| |
|
 |
CONTRIBUCIÓN DEL TIRO HORIZONTAL A LA
SÍNTESIS NEWTONIANA |
 |
|
|
|
|
| |
Una característica importante
de la
física
de Aristóteles (384 a. C.
- 322 a. C.) fue plantear una
separación radical entre dos "mundos": un mundo sublunar
imperfecto o terrestre y el mundo celeste o perfecto. Se
consideraba que estas dos partes del Universo funcionan obedeciendo a leyes
diferentes: en el mundo celeste, el Sol, la Luna y las
estrellas se mueven aparentemente de forma regular y permanente
siguiendo círculos suaves y uniformes alrededor de la
Tierra; en cambio, en el mundo imperfecto terrestre, el
estado natural de los objetos es el reposo, es necesario
intervenir sobre ellos para ponerlos en movimiento (y
para mantener dicho movimiento) y todos los objetos, lanzados con mayor o menor velocidad,
siempre caen al suelo y terminan parándose.
Con el establecimiento
de las leyes de la mecánica newtoniana y de forma
particular al formular la ley de gravitación,
Newton
(1643-1727)
declaró
el carácter universal de las leyes de la
mecánica y promovió una ruptura con la tradicional separación entre los
llamados "movimientos de objetos terrestres y celestes".
|
|
| |
|
|
| |
|
 |
|
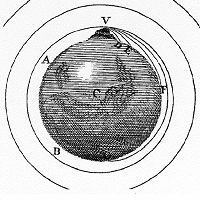
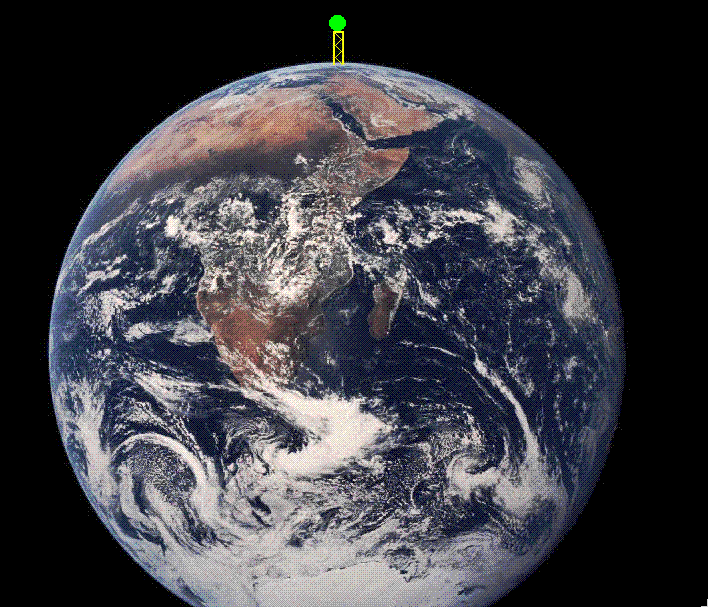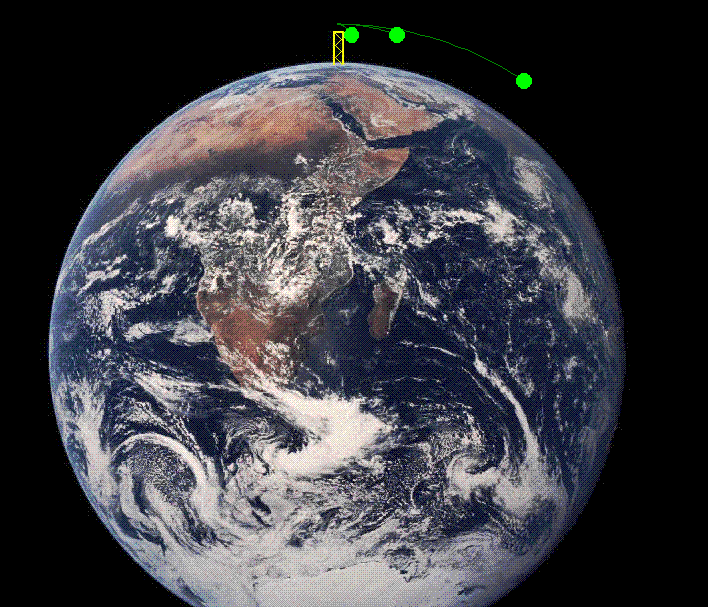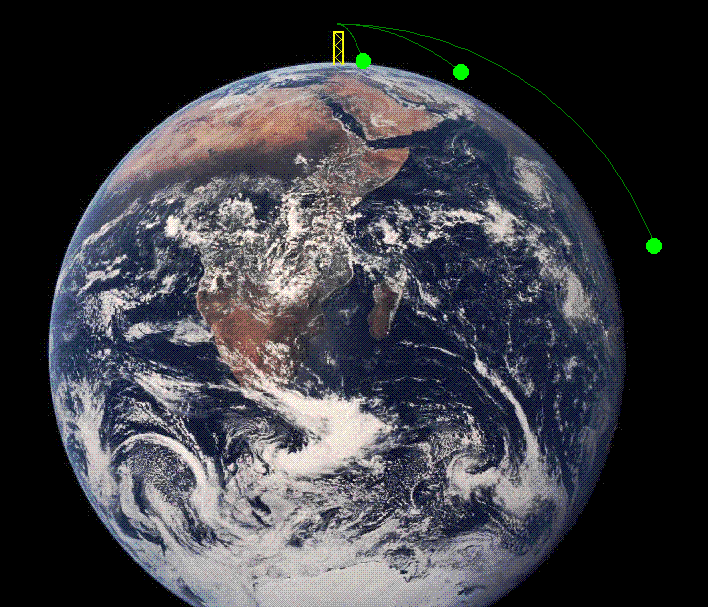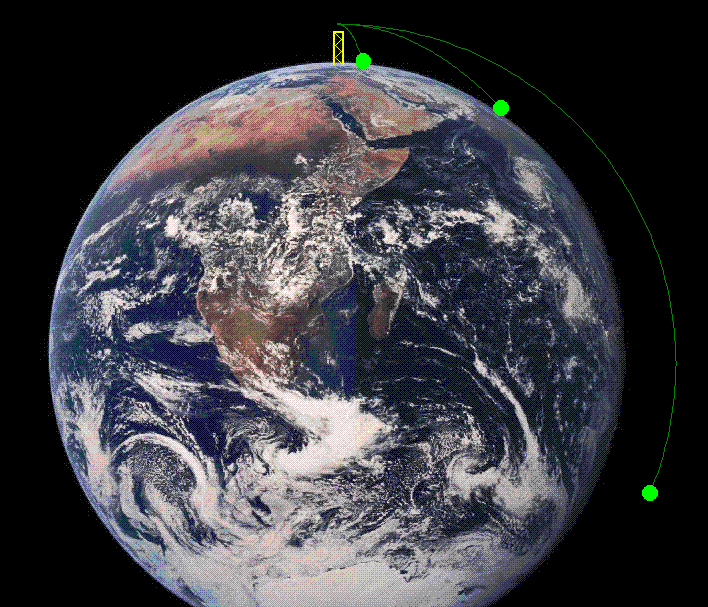
La
ilustración adjunta, similar al dibujo que encontramos en
la portada de muchas ediciones de los Principia de
Newton, ayuda a ver
la contribución que puede hacer el estudio del tiro
horizontal a la síntesis newtoniana. Un objeto lanzado horizontalmente desde una
colina V realiza un movimiento parabólico hasta caer
en un cierto punto D.
Si la velocidad es mayor, el mismo
objeto caerá en el punto E, F,.. Ahora bien, si la
velocidad del lanzamiento es bastante mayor, ocurrirá
para un cierto valor de ésta, que la relación entre su
movimiento de
avance horizontal y el de caída vertical coincida exactamente con
la relación existente entre el avance horizontal del suelo
terrestre y la caída de éste (se ha de tener en cuenta la
esfericidad de la Tierra) El objeto caerá entonces al mismo ritmo que "cae" el
propio suelo terrestre, con lo que siempre estará a la misma
altura y, por tanto, describirá una trayectoria circular alrededor
de la Tierra, como hacen los satélites. |
|
|
| |
|
|
| |
La siguiente
animación reproduce este razonamiento de Newton. |
|
| |
|
|
| |
|
 |
|
Vemos,
con ella, que no se plantean diferencias fundamentales
entre el movimiento regular de un satélite (un
movimiento "celeste") y el de un tiro horizontal que
termina chocando contra el suelo (un movimiento
"terrestre") cuando se interpretan bajo el paraguas de
las leyes de Newton.
Se requieren las mismas leyes
fundamentales para estudiar ambos movimientos y es
únicamente el valor de la velocidad inicial en relación
con la altura del lanzamiento lo que determina que el
objeto siga una trayectoria parabólica o circular.
Clic
aquí para descargar esta animacion.
Para abrirla y manipularla en tu ordenador descarga
Modellus |
|
|
| |
|
|
| |
Estos casos y los de otras trayectorias que también
son posibles bajo estas condiciones (órbita elíptica,
trayectoria hiperbólica abierta,..) se desarrollan con detalle
este apartado del tema dedicado al estudio del Campo
gravitatorio. |
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|

