| |
|
 |
TRES
PROBLEMAS QUE PONEN EN EVIDENCIA LA NECESIDAD DE ADOPTAR
SRI |
 |
|
|
|
| |
|
Vamos a comentar tres
problemas
en los que se pone en evidencia la
necesidad de
adoptar
convenientemente el SR,
con objeto de garantizar que sea inercial y se
puedan aplicar las leyes de la mecánica de Newton. |
| |
|
 |
Problema 1: La mujer del dibujo adjunto
se encuentra en el
interior de un ascensor
encima de
una balanza.
Estudia
lo que puede marcar la balanza cuando el
ascensor: a) Tiene velocidad constante. b)
Acelera.
Analiza
la
situación
desde dos
SR: interior
(ligado al ascensor) y exterior (ligado al
edificio en el que funciona el ascensor) |
|
| |
|
La balanza indica siempre la fuerza de
apoyo N entre dicha balanza y la propia mujer. Cuando el ascensor tiene un movimiento uniforme,
esta fuerza de apoyo es igual al peso de la mujer, pues,
la fuerza resultante que se ejerce sobre la mujer tiene
que ser nula, independientemente del SR escogido. Sobre
ella, se ejercen dos fuerzas iguales y
opuestas (el peso y la fuerza normal) y, al sumarlas, se compensan.
Esto es compatible con el hecho de que en el SRI
exterior el movimiento de
la mujer es rectilíneo y uniforme y en el SRI interior,
ligado al suelo, la mujer está en reposo.
Cuando el ascensor acelera
(en el momento de arrancar o
mientras se detiene)
la indicación de la balanza cambia, mostrando
un
incremento
o una disminución
de la fuerza de apoyo sobre el
suelo.
No existe dificultad en interpretar este hecho adoptando el punto de vista de
un SRI exterior: La modificación de
la fuerza de apoyo se debe a que la fuerza resultante sobre la mujer no es cero,
puesto que el ascensor (y la mujer) tiene aceleración.
En cambio, este mismo hecho
no se puede
explicar de forma satisfactoria si tratamos de usar las leyes de Newton
en
el
SR
ligado al ascensor (acelerado).
En este
SR,
ligado al ascensor,
la mujer
está en reposo, pero el hecho de que se modifique la
medición de la balanza, indica que la fuerza peso y la fuerza normal no se
compensan.
La fuerza resultante sobre la mujer no
es
cero y
ella, sin embargo,
estaría en reposo. |
| |
|
Problema 2:
Del techo de un
autobús
tren cuelga un péndulo.
¿Qué
ángulo forma con
la
vertical? |
| |
|
Mientras el autobús tenga una velocidad
constante (es decir, mantenga un movimiento
rectilíneo y uniforme, es adecuado estudiar el problema según
el punto de vista del SRI exterior y también
desde el SRI interior, ligado al tren. La fuerza resultante sobre la bolita del péndulo es cero
(se equilibran la fuerza peso y la tensión
de la cuerda) y la bolita
cuelga
en reposo
(SRI interior) o mantiene un MRU (SRI exterior). En cambio, cuando el
autobús
acelera
(aumenta o disminuye la rapidez y/o toma una
curva)
debemos adoptar obligatoriamente un SRI exterior
para interpretar el movimiento con las leyes de
Newton. En dicho SRI
se interpreta que el tren
tira de
la cuerda
y ésta, a su vez, tira de la bola.
|
|
| |
|
 |
|
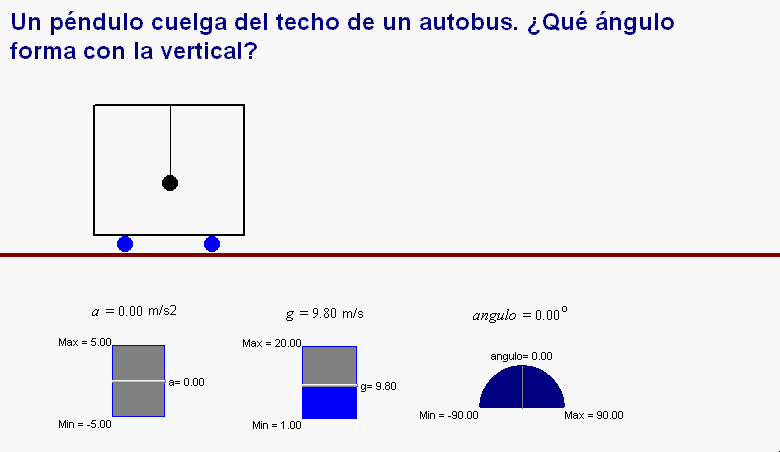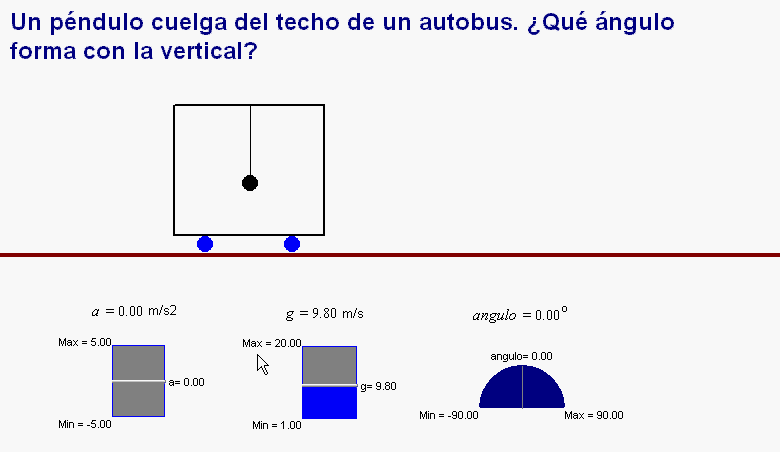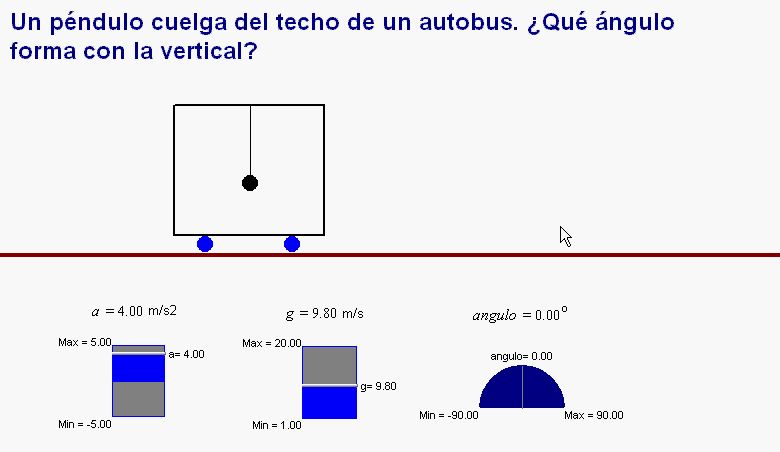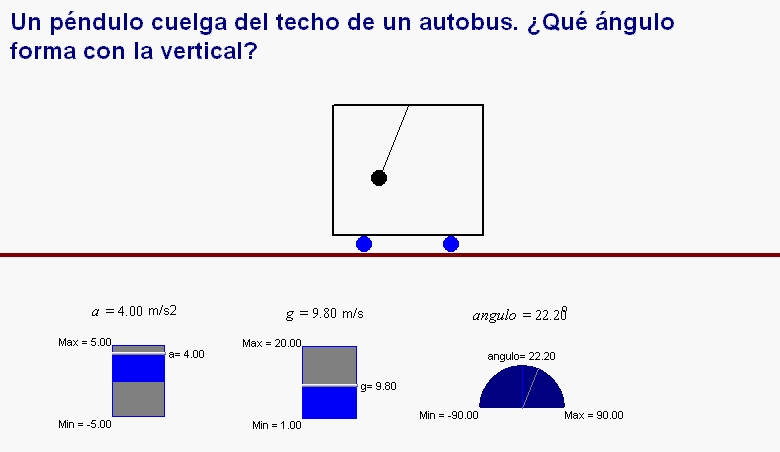
Así, por ejemplo, si la rapidez del
autobús aumenta, la bola
se
“retrasa” en su movimiento, lo que se traduce
en una desviación del péndulo respecto de la dirección
vertical.
Tal como muestra la animación adjunta, esta desviación permanece constante mientras
el vagón también mantenga una aceleración constante.
Clic
aquí para descargar la animación y
una resolución literal del problema.
Para
manipularla en tu ordenador, instala
Modellus |
|
|
|
|
Una vez más, resulta insatisfactorio cualquier
intento de interpretar la situación adoptando un SR no inercial, ligado al vagón.
Según este punto de vista, la suma
de las fuerzas que se ejercen sobre la bolita desviada de
la vertical (el peso,
vertical, y la tensión de la cuerda, oblicua) produciría
una fuerza resultante horizontal, y esto, a los ojos del
observador interior, es incompatible con un péndulo
desviado, pero en reposo (respecto del vagón) |
| |
|
Problema 3:
Describid el movimiento de un objeto que se coloca
encima de una plataforma circular giratoria, suponiendo
que gira con una velocidad angular, w, constante. |
| |
|
Para garantizar la aplicabilidad de las leyes de
Newton, adoptamos
un SRI exterior a la plataforma. Según
este punto de vista, la fuerza de rozamiento que
hace la plataforma sobre el objeto, le comunica
la velocidad de la plataforma. Si el objeto
gira solidariamente con ella, su aceleración es igual
a la aceleración centrípeta del movimiento
circular y uniforme: FN = m·aN
= m·w2·R. Esta expresión indica que cuanto más rápido gire la
plataforma, mayor sea la masa del objeto o más
al exterior se coloque, mayor
es la fuerza requerida para que el objeto gire solidariamente con la
plataforma. |
| |
|
¿Qué ocurre cuando la
fuerza de rozamiento no es suficiente para
mantener el movimiento circular? En ese caso, la
fuerza modifica la velocidad del movimiento del
objeto, pero no es suficiente para mantener la
distancia al centro. Si
de repente desapareciera el rozamiento, el
objeto seguiría con un movimiento rectilíneo y
uniforme a esa velocidad. El resultado visible
desde un SRI exterior es que
el objeto sale despedido hacia el
exterior de la plataforma giratoria. En algunos museos de ciencias hay plataformas en
las que se pueden realizar estos experimentos.
La fotografía adjunta corresponde a una visita al
museo de las artes y las ciencias de Valencia
realizada en 2006 por un grupo de alumnos del
IES "Leonardo da Vinci" de Alicante. |
|
 |
|
| |
|
También en este ejemplo, si tratamos de
describir lo que sucede desde
un SR
no inercial, ligado a
un
punto de la plataforma, las
predicciones de la mecánica de Newton no concuerdan con
el
movimiento real.
Si
el objeto colocado ahí dentro
es una persona y
quiere
permanecer quieto
deberá agarrarse a algún asidero para
evitar ser desplazado hacia el exterior. |
|
|
| |
Índice |
 |
|
|
|
|
|
|