MASA DE UN SISTEMA DE PARTÍCULAS

 
     
 

Una consecuencia notable del procedimiento seguido para la generalización de las leyes de la dinámica relativista a sistemas de partículas, es el hecho de que, en general, la suma de las masas individuales de las entidades componentes de un sistema no es igual a la masa del sistema entero. Para ver por qué ocurre esto vamos a analizar el sistema más simple, constituido por dos partículas que no interaccionan entre sí.

 

Lo primero que se ha de tener en cuenta es el hecho de que, globalmente, las dos partículas que componen este sistema simple sólo pueden estar en dos estados cinemáticos diferentes: a) En reposo relativo (significa que con respecto a cualquier sistema de referencia ambas tienen la misma velocidad, o que la velocidad de cualquiera de ellas es nula en el sistema de referencia ligado a la otra). b) En movimiento relativo (significa que en cualquier sistema de referencia no coinciden sus velocidades)
 

Vamos comprobar, utilizando diagramas impulso-energía, que en el primer caso (estado de reposo relativo) la masa de este sistema es igual a la suma de las masas de las dos partículas, mientras que en el segundo supuesto (estado de movimiento relativo) la masa de este sistema es mayor que la suma de las masas de las dos partículas.

 

La siguiente animación (debajo) ilustra el primer supuesto. Con las dos partículas en reposo relativo, sus cuadrivectores impulso-energía  tienen la misma inclinación en el diagrama (diferente en cada sistema de referencia). En el sistema de referencia ligado a las dos partículas los cuadrivectores son verticales (sus impulsos son nulos) y en cualquier otro sistema de referencia se inclinan por igual (tanto más cuanto mayor sea la velocidad de las partículas respecto de él). En estas condiciones, aunque la longitud aparente del cuadrivector impulso-energía del sistema cambia al cambiar de referencial, su módulo no lo hace (recuérdese el signo menos) y, en consecuencia resulta: msistc2 = m1c2 + m2c2 → msist = m1 + m2
 

 

 

 

Clic aquí para descargar esta animación. Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)
 

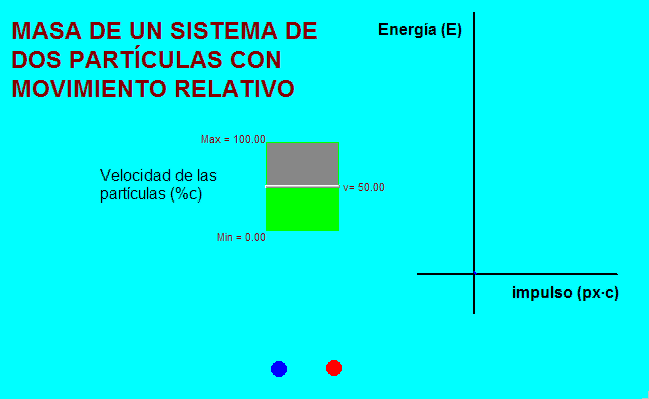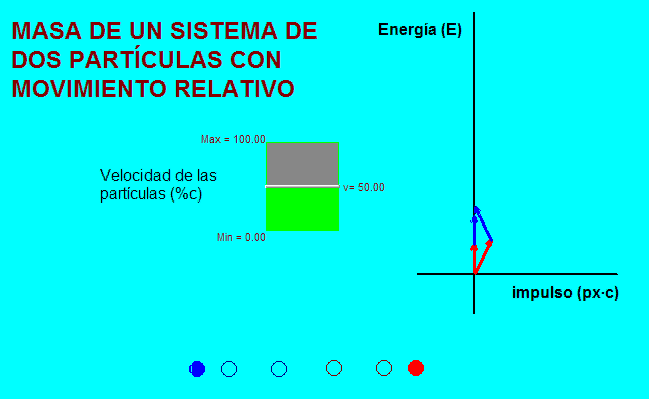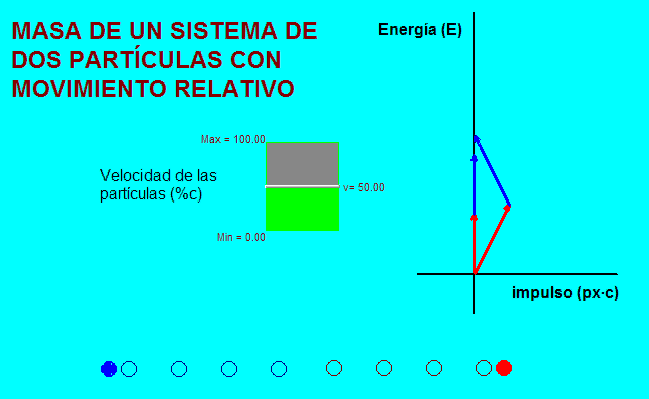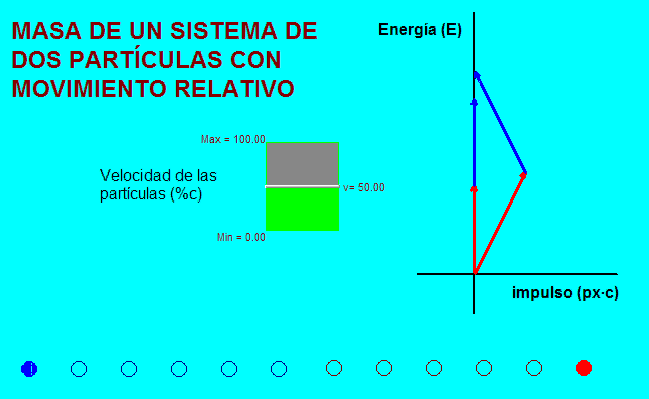
Para ver el segundo supuesto, vamos a elegir como segundo sistema de referencia para comparar con los sistemas de referencia ligados a cada partícula, aquél en el que ambas se alejan entre sí con velocidades opuestas de la misma magnitud.

 

 

Tal como muestra la animación adjunta (a la izquierda), con esta elección, que es siempre posible hacer, el extremo del cuadrivector que se obtiene después de sumar los dos impulsos-energía de cada partícula está en el eje vertical del diagrama en los dos sistemas de referencia adoptados. Esto permite comparar directamente el módulo de esa en el sistema de referencia exterior (msistc2), con el de esa misma suma en los sistemas de referencia ligados a ellas (m1c2 + m2c2) Se obtiene:

msistc2 > m1c2 + m2c2 → msist > m1 + m2

Es decir, en este caso, la masa del sistema es mayor que la suma de sus masas.

Clic aquí para descargar esta animación. Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)
 

En resumen, la masa de un sistema de dos partículas en movimiento relativo  es mayor que la suma de las masas de dichas partículas. Esta diferencia en la masa es tanto mayor cuanto mayor sea la la velocidad de una de las partículas con respecto a la otra.
 

Vamos a generalizar este resultado para aplicarlo a un gas ideal. Para ello imaginamos un proceso en el que, partiendo de una configuración hipotética del gas con todas sus moléculas en reposo (es decir, totalmente “frio”), se les va comunicando energía cinética hasta constituir el gas, tal como se muestra, por ejemplo, a la temperatura ambiente. Este proceso enseña que comunicar al gas en su conjunto la energía interna necesaria para calentarlo hasta alcanzar una determinada temperatura supone incrementar su masa. De hecho, aplicando formalmente las leyes de la relatividad se obtiene que la diferencia de masa es exactamente igual a su energía térmica (expresada en unidades de masa):
 

 

 

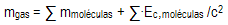
Este resultado de que la masa del gas es mayor que la suma de las masas de sus moléculas,  es consecuencia del hecho de que dichas moléculas se mueven libremente y se extienden para ocupar todo el volumen del recipiente que las contiene. El gas es un sistema de partículas libres (no ligadas). Como es lógico, al aplicar estos conceptos a los sistemas ligados (por ejemplo: una molécula, un átomo, un núcleo atómico, etc.) se obtiene el resultado opuesto: la masa del sistema es menor que la suma de las masas de sus componentes.
 
 
Así por ejemplo, la masa de un núcleo del isótopo Nitrógeno-14 se obtiene mediante el siguiente cálculo:
 

 

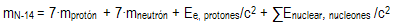En este caso, la diferencia de masa es negativa porque la fuerza nuclear entre los nucleones que la forman (7 protones y 7 neutrones) es de atracción y supera a las fuerzas de repulsión entre los protones (cargas del mismo signo). Esta diferencia negativa de masa es la energía de enlace que hay que vencer para romper el núcleo.