Para estudiar esta cuestión retomamos el ejemplo de las ondas que se pueden producir en la superficie de un lago. Estas ondas se transmiten en todas las direcciones de un plano horizontal (el de la superficie del agua), por lo que la energía transmitida se va repartiendo puntos de circunferencias concéntricas. Por lo tanto cada punto sólo recibe una porción de la energía original del foco, tanto menor cuanto más nos alejemos del origen de las vibraciones.

Este fenómeno se llama amortiguación y ocurre cuando la onda se propaga en varias direcciones. Lógicamente, la magnitud de la amortiguación depende de que la onda se propague en dos dimensiones (onda circular) o en tres (onda esférica).

En la animación adjunta se representa la propagación de una onda esférica. En este caso, la intensidad decae rápidamente al alejarnos del foco. Como la energía se ha de repartir en frentes de onda esféricos, la intensidad es inversamente proporcional al cuadrado de la distancia al foco.

Clic aquí para descargar esta animación [Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)]

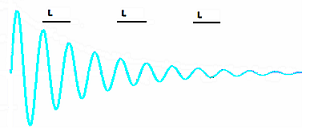
El dibujo adjunto representa un corte transversal de una onda amortiguada como las que se producen en la superficie del agua. Se señala una longitud L a diferentes distancias del foco, con objeto de dejar claro que la amortiguación supone una disminución de la amplitud, pero no de la longitud de onda. En la velocidad de propagación de la onda, c, sólo influye la capacidad del medio para transmitir la vibración (dicha velocidad es constante mientras la onda viaja por un medio determinado) La longitud de onda, l, se relaciona con la velocidad y con la frecuencia, n , según la expresión  c = l·n. Por tanto, todas las partículas alcanzadas por la onda oscilan con la misma frecuencia, n , y la longitud de onda no varía.