| |
|
 |
ESTUDIO
DEL MOVIMIENTO ARMÓNICO SIMPLE |
 |
|
|
|
|
| |
|
|
| |
|
 |
|
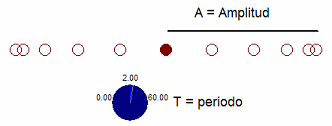
El movimiento de
oscilación más sencillo es el movimiento
armónico simple (MAS), que se repite periódicamente sin pérdida de
energía, es decir, manteniendo la amplitud
o máxima separación de la partícula oscilante respecto de
su posición de equilibrio. Dicha amplitud, A, y el
periodo, T (tiempo que tarda la partícula en realizar
cada oscilación completa) determinan el MAS. En lugar del
periodo, T, a menudo se caracteriza el MAS por la
frecuencia, f,
igual al número de oscilaciones realizadas en un
segundo. |
|
| |
|
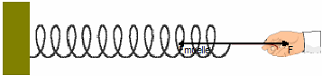
Para establecer la
fuerza que produce un MAS pensamos en un muelle
elástico, donde la fuerza que tenemos que ejercer para producirle una
elongación, x, se expresa mediante la ley de
Hooke (1635-1713)
es decir, es mayor cuanto mayor es
dicha elongación (Faplicada
= K·x, siendo K una constante que representa a la
elasticidad del muelle). |
| |
|
 |
|
Al estirar el
muelle, él tira de nuestra mano con una
fuerza de recuperación igual y de sentido
opuesto (Fmuelle
= -K·x). Después de soltarlo,
la fuerza de recuperación mantiene el
movimiento de oscilación. En estas condiciones, si el muelle fuera perfectamente
elástico, el movimiento de oscilación sería
armónico simple. |
|
| |
|
Las ecuaciones de un
MAS se
pueden obtener relacionando la fuerza de recuperación de
un muelle con la
aceleración y ésta con la velocidad y la elongación. Se
obtiene que las
tres magnitudes (posición, velocidad
y aceleración) tienen una dependencia sinusoidal respecto del tiempo,
siendo las gráficas que representan su evolución similares, si bien, la velocidad se
desfasa un cuarto de periodo respecto de la elongación
(la velocidad es nula en las posiciones extremas,
dónde es máxima la elongación), y la
aceleración se desfasa medio periodo respecto de la
elongación, siendo proporcional y de signo opuesto a
ésta (en todo momento, la fuerza y con ella la
aceleración, se opone a la elongación) |
| |
|
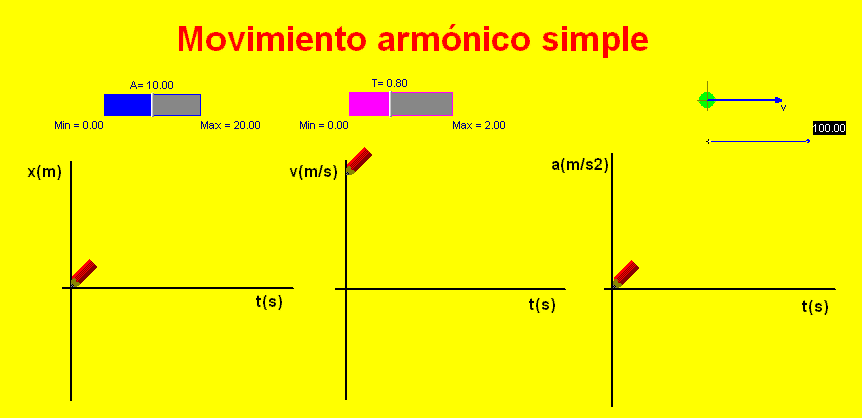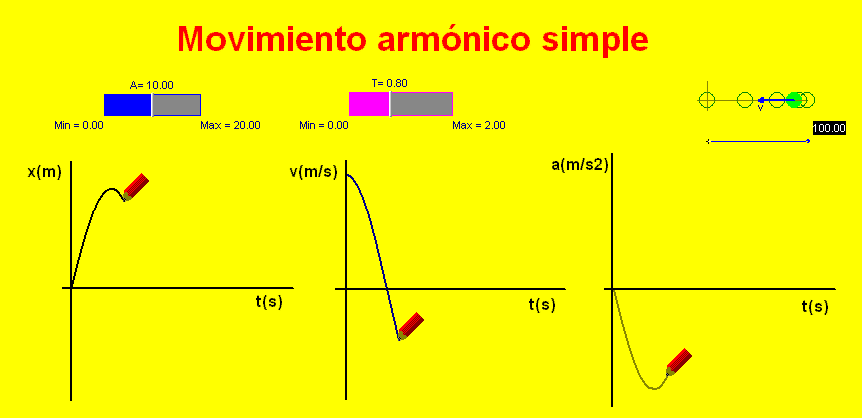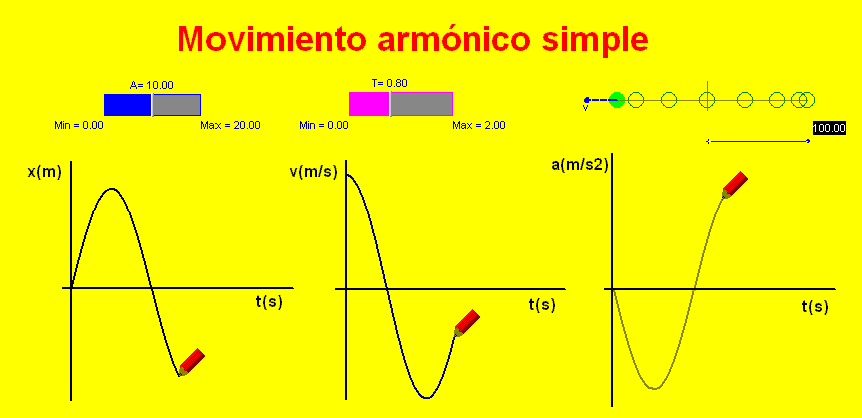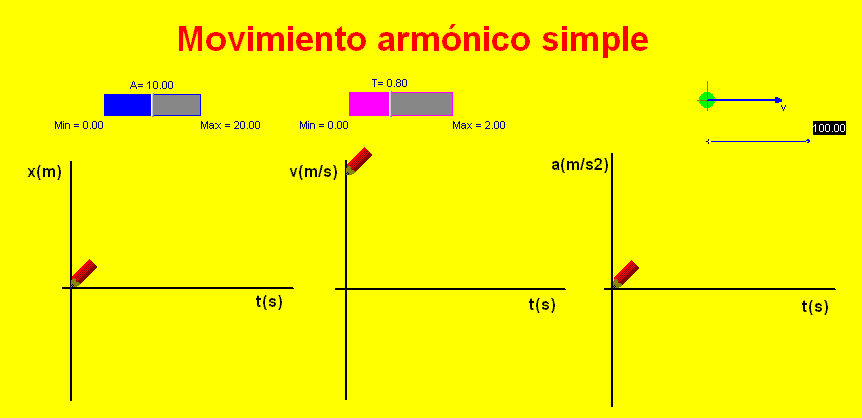
Para practicar estos
conceptos, hemos diseñado una animación interactiva Modellus que reproduce un
MAS y calcula y representa gráficamente la evolución de la posición, la
velocidad y la aceleración. Se pueden modificar los
parámetros que determinan el MAS (es decir, el
periodo y la amplitud del movimiento), comprobando cómo
afectan dichas modificaciones en el movimiento y sus
gráficas. |
|
|
|
 |
|
Clic
aquí
para descargar esta animación [Si no lo tienes instala
Modellus
2.5 (32 bits) o
Modellus 3 (64 bits)] |
|
|
| |
|
|
|