| |
|
 |
LEY DE
LA FUERZA DE LORENTZ Y SEGUNDA LEY DE LAPLACE |
 |
|
|
|
| |
|
 |
|
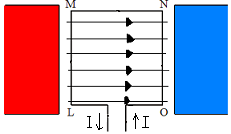
En la
posición indicada en el dibujo adjunto, el
campo magnético ejerce sobre la espira rectangular un par de fuerzas
que la hacen girar para alinearse con el campo. Tales fuerzas se ejercen sobre los conductores ML y ON:
La fuerza
magnética sobre el conductor ML es perpendicular al
plano de la espira y se dirige hacia nosotros, mientras la fuerza magnética sobre el tramo NO
es también perpendicular al plano de la espira y
se aleja de nosotros.
A medida que la espira va girando, el par de fuerzas va
siendo cada vez menor y cuando ha girado 90º cesa, porque en esa posición el campo
magnético creado por la espira está alineado con el
campo magnético producido por el imán. |
|
|
|
|
Del análisis de
este proceso particular cabe extraer las siguientes conclusiones
generales: |
|
|
|
1) La fuerza que
ejerce un campo magnético sobre corrientes paralelas a él (como, en este
ejemplo, los tramos de conductor MN y LO) o, más en general, sobre cualquier carga
móvil, cuya velocidad sea paralela al campo, es cero.
|
|
|
|
2) La fuerza que
ejerce un campo magnético sobre corrientes perpendiculares a
dicho campo (como, en este ejemplo, los tramos de conductor ML y ON) o, más en general, sobre cualquier carga
en movimiento, cuya velocidad sea perpendicular al campo es máxima.
|
|
|
|
3) Por tanto, la
magnitud de la fuerza magnética depende del ángulo, a,
que formen el vector velocidad, v, y el vector inducción
magnética, B; más precisamente es proporcional al seno de
dicho ángulo.
|
|
|
|
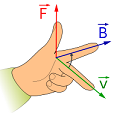
4)
Además, la
dirección de la fuerza magnética es perpendicular al
plano que contiene a los vectores v y B y
su dirección es la que indica la llamada regla del
sacacorchos, o regla de la mano izquierda, que se
ilustra en el dibujo adjunto. En dicho dibujo el sentido del vector velocidad, v, es el de
la corriente eléctrica, es decir, el del movimiento de cargas
positivas. Sobre cargas móviles negativas (por ejemplo,
electrones), la fuerza magnética se ejerce en sentido
opuesto al representado. |
|
 |
|
|
|
|
5) Lógicamente,
la magnitud de la fuerza magnética sobre una carga móvil, q,
o sobre una corriente, de intensidad, I, también es
proporcional a dicha carga, q, o a dicha intensidad,
I. |
|
|
|
|
|
Considerando este conjunto de
afirmaciones, la expresión operativa que calcula la fuerza
magnética Fm sobre una carga móvil es:
Fm = q (v x B)
Se
conoce como ley de la fuerza de
Lorentz (1853-1928)
en reconocimiento al científico holandés, que investigó
las acciones entre campos magnéticos y cargas
móviles. En esta ley, v x B,
es el producto vectorial de los vectores
velocidad (de la carga móvil) e inducción magnética. El resultado de
dicho
producto vectorial es un vector con las
propiedades exigidas por las afirmaciones de la
1) a la 4) que se acaban de exponer.
|
|
|
|
|
Cuando, en lugar de una carga móvil, se
tiene un conductor rectilíneo (de longitud, L),
recorrido por una corriente de intensidad, I, la fuerza
magnética sobre él es: |
|
|
|
Fm
= I (l x B) |
|
|
|
Esta expresión se puede
deducir de forma muy sencilla a partir de la ley de la fuerza de Lorentz
y se conoce como segunda ley de
Laplace (1749-1827). |
|
| |
Índice |
 |
|
|
|
|
|