|
 |
CONCEPTO
DE CAMPO GRAVITATORIO |
 |
|
|
| |
|
El
concepto
newtoniano de fuerza encuentra dificultad para
interpretar
las fuerzas ejercidas a distancia.
Podemos expresar esta dificultad mediante las siguientes preguntas: ¿Cómo es posible que
se ejerzan fuerzas dos
objetos
(por ejemplo, dos cuerpos celestes),
sin haber nada entre ellos?
¿Cuál puede ser
el mecanismo de la interacción?
|
|
 |
|
| |
|
En
relación con estas cuestiones, dos
siglos después de que Newton enunciara la
ley de
gravitación universal, se elaboró el
concepto de campo, que
rivalizó con la noción tradicional de fuerza y empezó a
desplazarla. Lo introdujo Faraday (1791-1867) para
interpretar las leyes que rigen las acciones entre
cargas, corrientes eléctricas, e imanes, y pronto se
mostró como
uno de los conceptos más fructíferos de
la física. |
|
|
|
Por
definición, el
campo gravitatorio (Eg) que produce un
cuerpo en un punto cualquiera es igual al cociente entre la fuerza
de atracción gravitatoria que dicho cuerpo ejerce sobre una
masa testigo o masa de prueba colocada ahí y el valor de dicha masa de
prueba. |
|
|
|
 |
|
|
Para
desarrollar de forma operativa esta
definición a la izquierda se ha representado la fuerza de atracción
gravitatoria que ejerce un cuerpo
celeste sobre un objeto de prueba. El módulo de dicha fuerza se calcula
con la
ley de gravitación universal:
|
| |
|
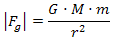 |
|
Donde M es la masa del
cuerpo celeste que produce el
campo, m es la masa del
cuerpo de prueba y r es la
distancia entre los dos objetos (medida
de centro a centro) |
|
|
|
|
|
|
Por tanto,
el módulo del campo gravitatorio que
produce el cuerpo de masa M en el punto donde se colocó la masa
testigo es: |
|
|
|
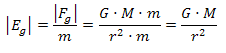 |
|
|
|
Esta
expresión dice que el
valor del campo gravitatorio no depende
de la masa testigo que se coloque en el
punto (m),
y sí de la masa (M) del cuerpo
celeste que crea dicho campo y de la
distancia (r) entre el punto y el centro de masas de
dicho cuerpo celeste. |
|
|
|
Así se sustituye una interpretación del fenómeno
en función de la interacción gravitatoria entre dos
cuerpos, por otra que atribuye el mecanismo de
la interacción al campo
creado por uno de ellos: El cuerpo celeste
(de masa M) perturba el espacio, creando un campo gravitatorio,
Eg, y, al
colocar en cualquier punto del espacio
perturbado otro
cuerpo (de masa m), se ejerce sobre él una fuerza proporcional a su masa y al
campo: Fg = m·Eg |
|
 |
|
|
|
|
El
cálculo del campo gravitatorio aporta un punto de
partida útil para el estudio de movimientos de objetos
en el Cosmos. Si se conoce el valor y la dirección del
campo gravitatorio en un punto, se conocen
automáticamente los de la fuerza que se ejerce ahí sobre
cualquier objeto de masa, m (Fg
= m· Eg), lo que permite
escribir la ecuación de su movimiento, y, resolviéndola,
prever su trayectoria. |
|
|
|
 |
|
Es interesante el resultado obtenido cuando se aplican estos conceptos al estudio del
movimiento de un cuerpo que se abandona en un lugar
equidistante de un sistema estelar binario. Si las masas
de las dos estrellas que componen dicho sistema son
iguales, la fuerza neta ejercida sobre el cuerpo de
prueba a lo largo la mediatriz del
segmento que une a las estrellas, se
dirige siempre hacia el punto central entre ambas.
Como consecuencia
de ello, el cuerpo realiza un movimiento de oscilación
alrededor de esa posición, como una especie de "yoyó
gravitatorio".
La animación
Modellus adjunta muestra esta situación.
Clic
aquí para descargar
esta animación. Para manipularla en tu ordenador
descarga
Modellus |
|