|
|
|
 |
|
RELACIÓN ENTRE LA FUERZA DE ROZAMIENTO AL DESLIZAMIENTO Y LA FUERZA
NORMAL |
|
|
| Experimentos
realizados por alumnos de Secundaria y de Bachillerato en el IES "Leonardo Da Vinci" de Alicante
|
|
|
| |
|
|
|
|
|
|
| |
|
PROPÓSITO DEL
EXPERIMENTO |
| |
|
|
|
En otro
estudio experimental sobre la fuerza de
rozamiento al deslizamiento de un bloque de
madera encima de las mesas del laboratorio,
los estudiantes registran el pico de fuerza
necesario para poner a deslizar el bloque y
obtienen el valor de la fuerza de rozamiento al
deslizamiento, que es igual a la fuerza
(constante) que han de aplicar al bloque para
arrastrarlo con velocidad constante.
La teoría dice que
esta fuerza de rozamiento depende de un conjunto
de factores representativos de las superficies
en contacto (rugosidad, material, etc..) y de la
fuerza de interacción entre ellas, N. Lo
que nos proponemos en este experimento es
comprobar el cumplimiento de esta segunda
dependencia, según la cuál la fuerza de
rozamiento debería ser proporcional a la fuerza
de interacción entre las superficies, siendo el
coeficiente de proporcionalidad el llamado
coeficiente de rozamiento,
μ. |
|
 |
|
|
|
| |
|
| |
|
 |
| |
|
DISEÑO EXPERIMENTAL |
| |
| |
|
El diseño experimental utiliza un bloque
de madera, el sensor de fuerza
(preparado para tirar del bloque y hacerlo deslizar) y un
conjunto de pesas, que se colocarán encima del cloque con objeto
de incrementar paulatinamente la fuerza de interacción entre el
bloque y la superficie. |
|
|
|
 |
|
Mientras el objeto desliza,
los estudiantes procuran tirar de él ejerciendo una
fuerza constante, adecuada para mantener
(después de arrancar) un
movimiento uniforme del bloque. Para
este
deslizamiento horizontal, la fuerza
de interacción entre las superficies,
N, ha de ser igual y de sentido opuesto a
la suma del
peso del bloque más las pesas agregadas
en cada ensayo, P. En
cada ensayo, se registra la pareja de
valores conformada con dicha fuerza de
apoyo, N, y la correspondiente
fuerza de rozamiento, fr.
Finalmente, se estudia la
representación gráfica de fr
en función de N, con objeto de
verificar si la
relación entre ambas fuerzas es lineal,
y, en ese caso, obtener el coeficiente
de rozamiento. |
|
|
|
|
| |
|
| |
|
 |
| |
|
RESULTADOS
GLOBALES |
| |
|
|
| |
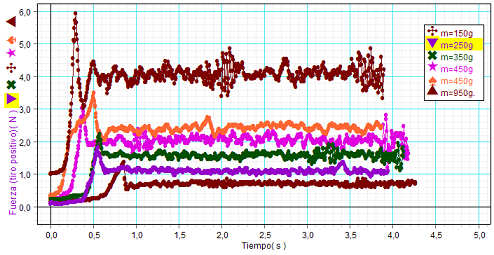
Adjunta se muestra en un solo cuadro un conjunto de seis gráficas
obtenidas por un grupo de alumnos en otros tantos ensayos
consecutivos. Para cada ensayo, los estudiantes colocaron encima
de un bloque de madera (de masa igual a 150 g) una pesa adicional
de 100 g.
Como se observa, todas las gráficas que obtuvieron tienen el
perfil esperado. Muestran una zona inicial,
con el objeto inicialmente en reposo,
en la que se aplica una fuerza creciente hasta el instante en el
que se consigue ponerlo en
movimiento
(pico de cada gráfica). Justo en ese momento, es decir, nada más
iniciarse el movimiento
la fuerza aplicada cae de forma bastante brusca. Seguidamente y
durante todo el deslizamiento la fuerza aplicada es bastante
estable, lo que indica que el movimiento del bloque es casi
uniforme y se puede considerar que la fuerza aplicada es igual y
opuesta a la fuerza de rozamiento. |
|
 |
|
| |
|
|
|
|
|
| |
|
 |
|
|
|
FUERZA DE ROZAMIENTO DE CADA ENSAYO |
| |
| |
|
 |
|
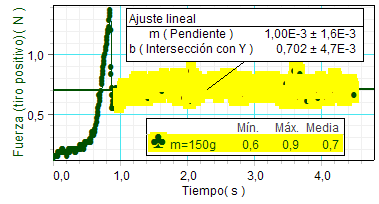
A la izquierda se muestra el análisis
realizado en la primera de las gráficas experimentales,
correspondiente el primero de los ensayos (deslizamiento
del bloque de madera, sin sobrepeso).
Por
un lado, se efectúa un
ajuste lineal de los valores empíricos de la fuerza aplicada en la zona de
deslizamiento. El ajuste confirma que es legítimo considerar dicha fuerza constante y aporta un valor de
ella de 0,7 N. Por otro lado, se
aplican las funciones estadísticas que aporta el
programa, que proporcionan los valores máximo (0,9 N), mínimo
(0,6 N) y medio (0,7 N) de dicha fuerza.
Estos valores corroboran su constancia y confirman
el valor de 0,70 N. |
|
|
| |
|
|
| |
Del mismo modo se obtiene el valor de la fuerza de rozamiento en
el resto de ensayos, cuyos análisis se muestran seguidamente,
usando las herramientas estadísticas. |
|
| |
|
|
| |
|
|
| |
|
|
|
| |
|
 |
| |
|
OBTENCIÓN DEL COEFICIENTE DE ROZAMIENTO |
| |
|
|
| |
|
 |
|
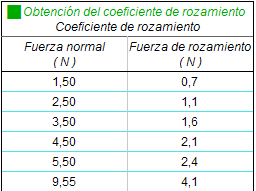
Se trata finalmente de verificar la ley del rozamiento
al deslizamiento:
fr =
μ·N
Se recogen en una tabla los valores experimentales de
ambas magnitudes. Los de la fuerza normal se calculan
teniendo en cuenta que en este caso dicha fuerza es
igual en cada ensayo al peso del bloque más las pesas
agregadas (para obtener los valores de la tabla adjunta
se ha redondeado g = 10m/s2). Los de la
fuerza de rozamiento son los obtenidos en el experimento
recién relatado. |
|
|
| |
|
|
| |
|
 |
|
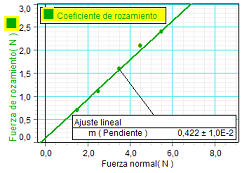
Puesto que la ley que se quiere verificar implica una
relación de proporcionalidad entre la fuerza normal y la
fuerza de rozamiento, se realiza un ajuste lineal de la
gráfica experimental de la relación entre ellas [fr
= f(N)].
Como se observa, dicho ajuste confirma la hipótesis y
permite obtener el valor de coeficiente de rozamiento,
en este caso:
μ = 0,42 |
|
|
| |
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Te puedes descargar los
resultados
originales del experimento descritos
en esta página.
Para abrir el archivo se necesita el programa DataStudio, del que tienen
licencia bastantes Departamentos de Física y Química de
institutos de Enseñanza Secundaria. |
|