|
|
|
 |
|
MOVIMIENTO ARMÓNICO SIMPLE
CON SENSORES - ESTUDIO DINÁMICO |
|
|
| Experimentos
realizados por alumnos de ESO y de Bachillerato en el IES "Leonardo Da Vinci" de Alicante
y en la Ikastola "Pasaia-Lezo" de Guipuzcoa
|
|
|
| |
| |
 |
OBJETIVOS Y DISEÑO
EXPERIMENTAL |
 |
RELACIÓN
ENTRE LA FUERZA Y LA POSICIÓN |
 |
CÁLCULOS EN
EL ANÁLISIS DINÁMICO |
 |
CAMBIO DE
MUELLE Y DE MASA COLGANTE |
 |
RESULTADOS DE
UN GRUPO DE PROFESORES |
 |
ARCHIVOS DE
DATA-STUDIO |
|
|
|
|
|
|
|
|
|
|
|
|
OBJETIVOS Y DISEÑO
EXPERIMENTAL |
| |
| |
|
Nos proponemos completar
el estudio
experimental del movimiento armónico simple
(MAS) en
su vertiente cinemática, con un estudio de
índole dinámica, es decir, incluyendo análisis
que consideran la fuerza que interviene en este
movimiento y su relación con las magnitudes
cinemáticas y con otras propiedades como, por
ejemplo, la constante elástica del muelle.
|
| |
|
 |
|
Para obtener mediciones
directas de la fuerza del MAS y de su evolución,
se prepara un montaje experimental como el que se
observa en la imagen adjunta, donde vemos a un
alumno realizando el experimento.
Este montaje tiene en
consideración que, al colgar del sensor de
fuerza el muelle, la fuerza de recuperación
ejercida por él se ejerce
tanto sobre el cuerpo que cuelga, como sobre el
sensor. Por tanto, durante las oscilaciones el
sensor registra la evolución con el
tiempo de la fuerza responsable del MAS. |
|
| |
|
|
|
|
| |
|
 |
| |
|
RELACIÓN ENTRE LA
FUERZA Y LA POSICIÓN |
| |
|
|
| |
|
Como la fuerza es
proporcional a la aceleración y la
teoría del MAS prevé que ésta, a su vez,
ha de ser proporcional y de sentido opuesto a la
elongación, las gráficas de la fuerza y de la
posición deberían mostrar perfiles opuestos.
|
| |
|
 |
|
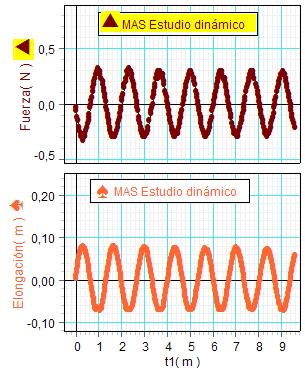
Para comprobarlo, los
alumnos añaden el sensor de movimiento
al montaje que se acaba de describir,
quedando el conjunto como muestra la
fotografía adjunta (izquierda). Con este
montaje obtienen, en primera
instancia, las gráficas de la fuerza de
tiro del muelle sobre el sensor de
fuerza y de la posición con respecto al
sensor de movimiento.
Después de
efectuar los cambios de variable
oportunos, los equipos obtienen las
gráficas de la elongación y de la fuerza
de recuperación. Estas gráficas (a la
derecha) confirman las predicciones,
mostrando que
en cada instante la elongación opuesta a la fuerza.
Conviene saber, por otra parte, que dividiendo los valores empíricos de la
fuerza entre la masa del cuerpo
colgante (se
puede medir usando el propio sensor de
fuerza) se obtiene una secuencia de
valores de la aceleración mucho más precisa que
la obtenida
en el
estudio cinemático.
Los valores experimentales de la fuerza
proceden de mediciones directas de
esta magnitud. En cambio los valores
de la aceleración, obtenidos en la
vertiente cinemática del experimento, los calcula el
programa a partir de los de la velocidad
y éstos a su vez los obtiene a partir de
los valores experimentales de la
posición (sin descartar ninguno). |
|
 |
|
|
|
| |
|
|
| |
|
 |
|
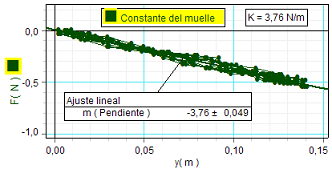
Para completar el estudio los alumnos
representan en una sola gráfica la relación entre la
fuerza de recuperación del muelle y la elongación.
Como
se observa, dicha representación confirma la ley de Hooke, según la cual la fuerza es proporcional, pero de
sentido contrario a la elongación. La constante de
proporcionalidad o, lo que es lo mismo, la pendiente de
la recta representada, es la constante de recuperación
del muelle, en este caso igual a 3,76 N/m. |
|
|
| |
|
|
|
| |
|
 |
| |
|
CÁLCULOS EN EL
ANÁLISIS DINÁMICO |
| |
| |
|
 |
|
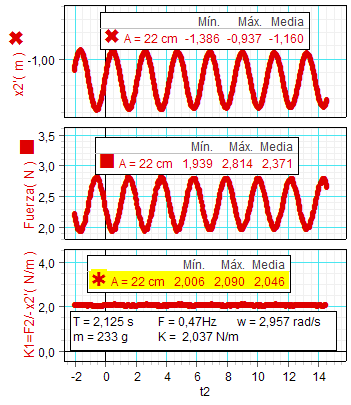
La figura adjunta (a
la izquierda), procede de uno de los
ensayos del sensacional experimento
enviado por el profesor Etxaniz y
muestra conjuntamente las gráficas de la
elongación, de la fuerza y de la
relación entre ambas magnitudes. Antes de
representar estas gráficas, se ha hecho
un cambio de origen en el tiempo
para eliminar el desfase
temporal y otro en la posición para restar
la distancia del sensor a la posición de
equilibrio del muelle y la
distancia del origen del muelle a la
posición de equilibrio del bloque que lo
estira (o, dicho de otro modo, la
longitud del muelle cuando el bloque
está en equilibrio). Así, la
magnitud representada, x2', indica
la elongación del muelle en cada
momento, y el cociente entre la fuerza y
dicha elongación es la constante del
muelle. Dicho cociente, calculado en
cada punto (usando la opción de calcular
que ofrece el programa), es lo que se
representa en la otra gráfica.
Como se
observa, se obtienen valores acordes con
su significado físico, puesto que dicho
cociente es aceptablemente constante a
lo largo de todas las mediciones, de las
que se deriva un valor de
2,046 N/m (valor medio de la
estadística). Es interesante comparar
este valor con el que se puede obtener
de forma independiente usando la expresión K = m·w2,
donde la masa m incluye al muelle (no
despreciable) y al bloque que cuelga, y
la pulsación w se obtiene
experimentalmente a partir del periodo.
Tal como se indica en el cuadro de
texto, el resultado, por este
otro procedimiento es K = 2,037, muy
próximo al anterior. |
|
|
|
|
En este
experimento se realizaron cuatro
ensayos diferentes y con diferente amplitud.
A todos les es aplicable la expresión
K = - m·w2 y los cuatro ensayos se realizaron con el mismo
muelle (y colgando de él la misma masa). Por
tanto, la pulsación w y el periodo T de todos
debe ser igual. |
|
|
|
 |
|
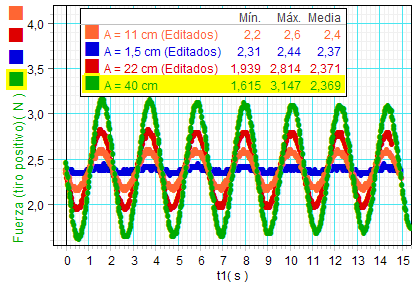
Para comprobarlo, se
representan las cuatro fuerzas bajo los
mismos ejes (después de haber cambiado
el origen de tiempos en todas para
eliminar el desfase temporal),
y se obtiene la elocuente gráfica adjunta,
donde:
1) Queda muy clara
(cualitativamente) la relación F = - K·x,
puesto que a los ensayos con mayor amplitud
les corresponde una mayor oscilación en
el valor de F.
2) Como consecuencia
de esta proporcionalidad entre F y
x,
las fuerzas varían sinusoidalmente con
el tiempo y lo hacen todas con
el mismo periodo (T = 2,125 s) que ya se
había medido en el
estudio cinemático
utilizando las gráficas de la posición.
3) Lógicamente
el valor de la fuerza en la posición de
equilibrio también coincide en los cuatro ensayos. Dicho valor lo da el
valor medio de la fuerza, obtenido con la
función estadística (alrededor de
2,37 N). |
|
|
|
|
Además de hacer estas
comprobaciones en el estudio comparativo de los
cuatro ensayos, en cada uno de ellos se obtuvo
de manera independiente el valor de la constante
del muelle, por el procedimiento que hemos
indicado un poco más arriba (para el MAS de
amplitud 22 cm). Los resultados resultaron
extraordinariamente precisos al diferir el valor
experimental de la constante en órdenes de
magnitud del 1-2 % entre unos ensayos y
otros (por ejemplo, para el MAS de amplitud 40 cm
se obtuvo K = 2,01 N/m) |
|
|
|
|
|
|
|
|
|
 |
|
|
|
CAMBIO DE
MUELLE Y DE MASA COLGANTE |
| |
| |
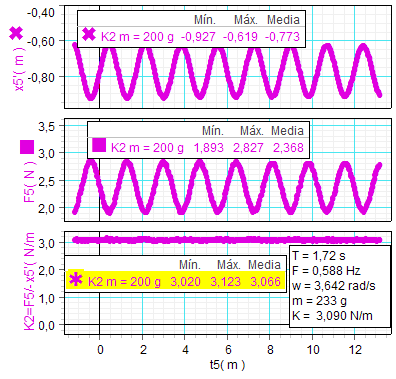
| Para completar el
estudio dinámico, se repitieron los
ensayos, primero sustituyendo el muelle
por otro y, después, modificando la masa
del cuerpo que cuelga. |
| |
|
 |
|
A la
izquierda se muestran los
resultados obtenidos al
sustituir el muelle anterior, 1,
por otro de "mayor rigidez", 2,
tal como se observa en las
fotografías adjuntas (debajo),
ya que la elongación del muelle
2 es menor para el mismo bloque.
Confirmando
las predicciones teóricas, se
obtiene un valor diferente y
mayor de la constante (K2
=
3,090 N/m,
calculado, o K2 =
3,066, "estadístico"), que el
obtenido en el ensayo que se
comenta en el apartado anterior
(K1 = 2,046
N/m)
Puesto que
K = - m·w2, también son
diferentes la pulsación,
que ahora es mayor (w2
= 3,642 rad/s; w1 =
2,957 rad/s) y el periodo,
que ahora resulta menor (T2
= 1,72 s; T1 = 2,125 s). |
|
|
|
|
|
 |
|
|
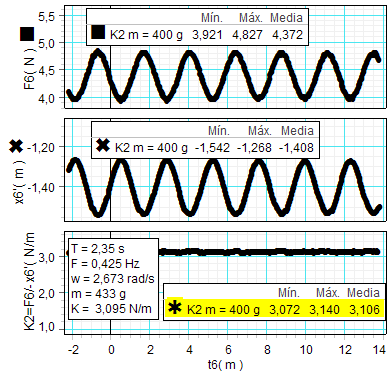
Por último,
se realizó otro ensayo
manteniendo este segundo muelle
y modificando la masa que cuelga
de él, a base de añadir pesas de
100 g sobre el bloque, tal
como se observa en la fotografía
adjunta (debajo a la derecha).
Lógicamente, la posición de
equilibrio es así mucho mayor y
también lo es el valor de F
en dicha posición. |
| |
|
|
|
A la
izquierda se muestran los
resultado, que, de entrada,
dejan en evidencia que, puesto
que no se cambió el muelle, la
constante K es la misma
que antes: Se obtiene K2
= 3,095 N/m, casi igual que
el valor de la otra experiencia
(3, 090 N/m).
Por otra
parte, como K = m·w2,
al aumentar la masa del bloque
el periodo T resulta
mayor que antes (ahora T =
2,35 s) y la pulsación w
menor (w = 2,673 rad/s).
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
RESULTADOS EN UN CURSO DE FORMACIÓN
DOCENTE |
| |
| |
|
 |
|
Con objeto de facilitar al
profesorado de física y química un acceso a los
conocimientos y a la metodología empleados en la
realización de trabajos prácticos de física con
sensores, hemos realizado cursos de formación docente
en institutos, universidades y centros de
formación del profesorado.
Adjuntamos ahora
resultados obtenidos por profesores en un curso
de formación impartido en Alicante en 2009. |
|
| |
|
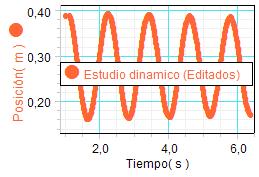
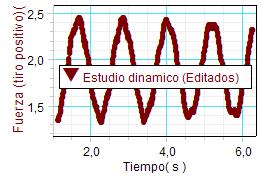
En este caso, los profesores realizaron un
estudio dinámico del movimiento armónico simple
en el que obtuvieron las
gráficas de la evolución de la posición
y de la fuerza (comprobando que son
opuestas), encontraron las ecuaciones del
movimiento de oscilación, etc. |
|
 |
|
 |
|
| |
|
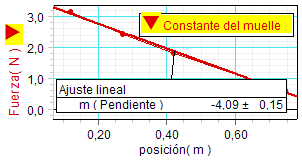
Adicionalmente
realizaron algunas medidas estáticas de
la fuerza y de la elongación y,
teniéndolas en cuenta, aplicaron la ley
de Hooke (F = - K·x) para obtener
la constante del muelle. |
|
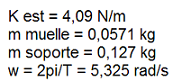 |
|
 |
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Puedes descargar los
resultados
originales de los experimentos que se
describen en esta página y en la dedicada al
estudio cinemático del MAS. Para abrirlos se necesita el programa DataStudio, del que tienen
licencia bastantes Departamentos de Física y Química de
institutos de Enseñanza Secundaria. |
|