|
|
|
 |
|
MOVIMIENTO ARMÓNICO SIMPLE
CON SENSORES - ESTUDIO CINEMÁTICO |
|
|
| Experimentos
realizados por alumnos de ESO y de Bachillerato en el IES "Leonardo Da Vinci" de Alicante
y en la Ikastola "Pasaia-Lezo" de Guipuzcoa
|
|
|
| |
|
|
|
|
|
|
|
|
|
PRODUCCIÓN DEL
MOVIMIENTO ARMÓNICO SIMPLE |
| |
| |
|
Después de desarrollar en clase la
teoría
sobre el movimiento armónico simple (MAS), deseamos estudiar experimentalmente un movimiento
real con estas características. Como
material de partida se dispone de muelles y se propone a los
estudiantes que elaboren un diseño experimental adecuado para
producir un MAS y estudiarlo empíricamente. |
| |
|
|
| |
|
|
|
|
| |
|
 |
| |
|
DISEÑO EXPERIMENTAL |
| |
|
|
| |
|
 |
|
La experiencia acumulada en el
trabajo con sensores de movimiento, enseña que para
determinar posiciones con mayor precisión conviene que
la superficie del móvil que se enfrenta al sensor sea
plana y perpendicular a la dirección del movimiento.
Por
tanto, se sustituye la bola por una base circular,
sujetada con con un ganchito que permite colgarla del
muelle y se coloca el sensor de movimiento en el suelo,
enfocado hacia la base plana del móvil.
En cuanto a la configuración del sensor, se obtienen resultados
excelentes trabajando en el rango de 40-50 Hz (40
o 50
mediciones por segundo) |
|
|
|
|
|
| |
|
 |
| |
|
GRÁFICAS DE LAS
MAGNITUDES CINEMÁTICAS |
| |
| |
|
 |
|
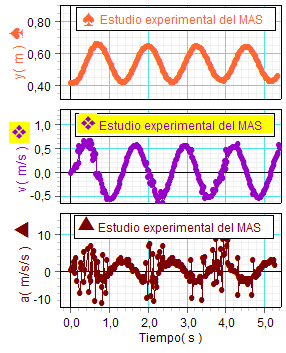
A la
izquierda se muestran las
gráficas experimentales de las
magnitudes cinemáticas
obtenidas por uno de los equipos
de alumnos en el laboratorio del
Instituto. Su perfil
corresponde a un movimiento armónico simple y se observa una
mayor imprecisión en
la gráfica de la velocidad y,
mucho mayor, en la de aceleración.
Esto se debe a una acumulación progresiva de
errores que comete por el programa al ir obteniendo las
magnitudes derivadas, ya que calcula
los valores de la velocidad a partir de los valores experimentales
de la posición (sin descartar ninguno) y los de la
aceleración a partir de los de la velocidad.
Los
alumnos presentan las tres gráficas conjuntamente para
facilitar la discusión
cualitativa de detalles
conceptuales del movimiento armónico
simple: 1) La velocidad es
máxima (positiva o negativa) cuando la posición
es nula, es decir, cuando el móvil pasa por la
posición de equilibrio; y es nula cuando la
posición es máxima o igual a la amplitud
(positiva o negativa), es decir, cuando el móvil
pasa por las posiciones extremas. 2) La gráfica
de la aceleración es similar
y de signo opuesto a la de la posición, como
corresponde a que la fuerza de recuperación
del muelle responsable de dicha aceleración se
opone en cada instante a la elongación.
Por
tanto,
dicha aceleración es máxima positiva cuando la
posición es igual a la amplitud negativa y
máxima negativa cuando la posición es igual a la
amplitud positiva. |
|
|
|
|
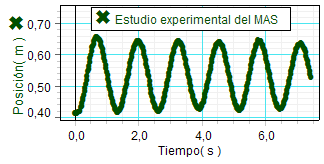
Por otra parte,
observando con un poco más de detalle
cualquiera de las tres gráficas, como,
por ejemplo, la de la posición (a la
derecha) se aprecia también que en el
movimiento estudiado se produce una ligera
amortiguación.
Aunque lo hace
muy lentamente, la amplitud
disminuye paulatinamente en cada
oscilación respecto de la
anterior. |
|
 |
|
| |
|
|
|
|
|
|
|
 |
|
|
|
CAMBIO DEL SISTEMA
DE REFERENCIA Y ECUACIÓN DEL MAS |
| |
|
|
|
Para obtener las
ecuaciones del movimiento, procede realizar un ajuste
sinusoidal sobre las gráficas de las tres
magnitudes cinemáticas. |
| |
|
 |
|
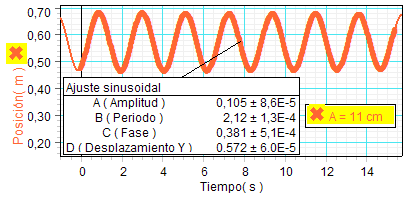
A la izquierda se
expone el resultado de dicho ajuste
sobre la gráfica de la posición obtenida
en el experimento que nos envía el
profesor Mikel Etxaniz, de la Ikastola "Pasaia-Lezo"
en Guipúzcoa.
Junto con la amplitud y el periodo, el programa
proporciona otros dos coeficientes: Uno,
C,
que llama fase y en realidad representa
el tiempo que falta hasta que el bloque
pase por la posición de equilibrio por
primera vez en sentido ascendente (es
decir, hasta que la fase pase por el
origen o tenga el valor de 2π),
y otro, D, que es el desplazamiento vertical,
o, lo que es igual, la distancia
entre el sensor y la posición de
equilibrio.
|
|
| |
|
Si se dejan los resultados y
su representación gráfica así, nos vemos obligados a trabajar en
un sistema de referencia incómodo, con origen
espacial en la posición del sensor y adoleciendo
de un desfase
temporal con respecto al instante en el que el
objeto pasa por la posición de equilibrio. Para evitar esta
incomodidad,
interesa realizar consecutivamente dos cambios de variable
(opción que facilita el programa entrando en la pestaña de
"Calcular"): |
| |
|
 |
|
1) En la posición,
para definir la elongación y
igual a la posición que mide el sensor menos el
desplazamiento vertical (en este caso yelongación = ysensor
- 0,572).
2) En el tiempo, para hacer
coincidir el inicio del tiempo con el
inicio de un ciclo, al pasar el móvil
por su
posición de equilibrio (en este caso,
tsin desfase = tsensor
- 0,381)
(Para hacer este cambio hay que definir
antes el tiempo como variable).
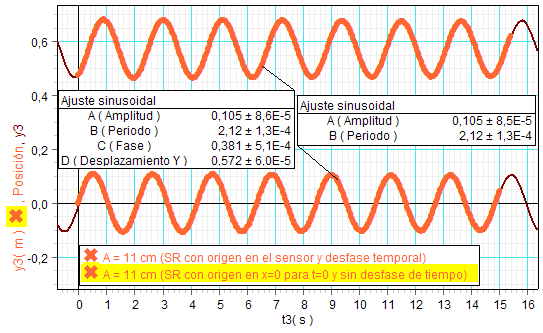
Después de haber definido las magnitudes
(elongación y tiempo sin desfase), se
presentan conjuntamente la gráfica
inicial (arriba) y la obtenida de la
elongación sin desfase (debajo). En esta
segunda, los coeficientes C y D son
prácticamente iguales a cero, es decir,
para t = 0 es y = 0, con
lo que la ecuación del movimiento se
escribe sencillamente:
y = A sin
(w·t)
y =
0,105 sin
(2π/2,12)·t
(en el ejemplo mostrado) |
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
CÁLCULOS
INTERESANTES |
| |
| |
|
Es muy interesante completar
las observaciones cualitativas que se han
realizado al comparar los
perfiles de las gráficas de las magnitudes
cinemáticas, con algunos cálculos dedicados a
confirmar predicciones de la
teoría sobre el movimiento armónico simple. |
| |
|
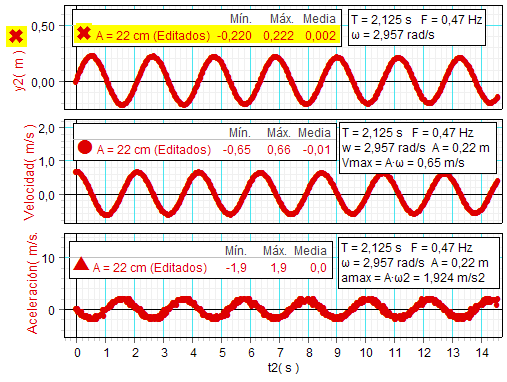
A la derecha se
muestran gráficas de la elongación, la
velocidad y la aceleración (todas
expresadas en el SR con origen en x =
0
y sin desfase temporal) para uno de los
ensayos del experimento enviado por el
profesor Etxaniz. Las funciones
representadas tienen excelente calidad
(no hay apenas deformaciones) y se ha
realizado un conjunto de comprobaciones
cuantitativas de mucho interés.
Concretamente se
calcula la pulsación w a partir
del periodo
T medido experimentalmente (w =
2π/T
= 2π/2,125
=
2,957 rad/s)
y, a partir de ella, se
obtiene a su vez la
velocidad máxima vmax
(vmax = A·w =
0,22·2,957
= 0,65 m/s).
Después de hacer
este cálculo, con la gráfica de la
velocidad activada, se usa la aplicación
del programa "Estadística" que enseña la velocidad mínima,
máxima y media, comprobando, como se
observa (valor mínimo de - 0,65 m/s
y valor máximo de 0,66 m/s),
que coincide plenamente con el calculado
por el otro procedimiento.
Lo mismo se
hace con la aceleración máxima (amax
= A·w2 =
0,22·2,9572
= 1,924 m/s2)
cuyos valores "estadísticos" máximo y
mínimo resultan en en este caso
±1,9
m/s2. |
|
 |
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
OSCILACIONES CON
DIFERENTE AMPLITUD |
| |
|
|
|
Para poner la guinda al
estudio cinemático del movimiento armónico
simple, es muy instructivo plantear a los estudiantes qué suponen
que cambiará si se estira más (o menos) el
muelle al iniciar el movimiento. Para ellos, resulta
evidente que la amplitud del movimiento va a ser
mayor (o va a disminuir), pero no es nada fácil
que prevean lo
que ocurre con el periodo, la frecuencia y la
pulsación. |
| |
|
 |
|
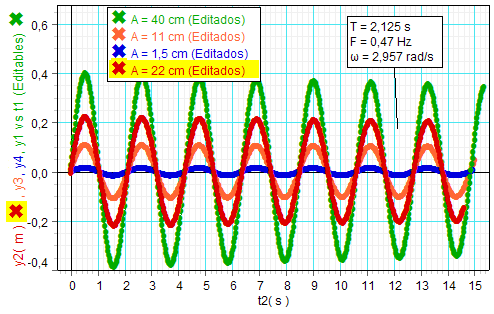
Las gráficas adjuntas
también pertenecen al
experimento del profesor Etxaniz y
muestran con altísima precisión que con
el cambio de amplitud, el periodo
(y por tanto, también la pulsación y la
frecuencia) de oscilaciones de
amplitudes diferentes, provocadas en el
mismo muelle (con el mismo cuerpo colgando
de él), es exactamente igual para todas
ellas.
Así se deduce si se realiza un
análisis dinámico del
movimiento (de dicho
análisis se obtiene la relación K = m·w2,
que indica que la pulsación w no varía
mientras no varíe el muelle K y/o
la masa m), pero no es, desde
luego, nada evidente a la intuición.
Es
una situación similar a la del periodo del movimiento
de oscilación del péndulo simple, donde la amplitud
no influye en el periodo, porque aunque la
oscilación de mayor amplitud supone un
desplazamiento mayor (por ello, se podría
pensar que el periodo también será
mayor), dicho desplazamiento se realiza
con cambios más rápidos de
velocidad. |
|
|
|
|
Como vemos, la justificación
de estos últimos resultados tiene su origen en
un estudio
dinámico del MAS. Dedicamos otra página a
dicho estudio, en el que se obtienen otras
consecuencias y resultados de interés. |
|
|
|
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Puedes descargar los
resultados
originales de los experimentos que se
describen en esta página y en la dedicada al análisis dinámico
del MAS. Para abrirlos se necesita el programa DataStudio, del que tienen
licencia bastantes Departamentos de Física y Química de
institutos de Enseñanza Secundaria. |
|