EQUILIBRIO TÉRMICO CON MODELLUS
 
 
 
Experimento realizado por estudiantes de Bachillerato en el IES "Leonardo da Vinci" de Alicante
     
     
 

PLANTEAMIENTO Y PROPÓSITO DEL EXPERIMENTO

  
     
 

La gráfica adjunta procede de un experimento realizado en marzo de 2010 en el Centro de Profesores y Recursos de Benidorm (la sesión la impartió el profesor Vicent Soler del IES "Sixto Marco de Elche")

 
     
 

 

Los profesores usaron agua caliente (obtenida después de calentar agua del grifo con un mechero "Bunsen") y agua fría (obtenida después de mezclar agua del grifo con cubitos de hielo).

Echaron el agua fría y el agua caliente a dos vasitos y, después de colocarlos dentro del calorímetro, midieron la evolución de las temperaturas.

Como se observa, se tardó algo más de 12 minutos en alcanzarse el equilibrio térmico entre ambas masas de agua.
 

Para analizar los datos con el software de los sensores se realizaron ajustes definidos por el usuario que aplican las leyes de enfriamiento y de calentamiento.
 
 
     
 

Cuando se realiza en clase este mismo experimento, los alumnos de Secundaria o de Bachillerato plantean hipótesis correctas sobre los procesos de enfriamiento y de calentamiento, hacia el equilibrio térmico. En Bachillerato, además,  estas hipótesis se plasman a través de sendas expresiones diferenciales sobre la evolución de la temperatura de las masas de agua (la que se enfría y la que se calienta). Pero, los estudiantes no tienen nivel suficiente de matemáticas para pasar de las expresiones diferenciales a las ecuaciones correspondientes, ni menos aún, para resolver dichas ecuaciones. Por este motivo, nos proponemos aquí realizar un análisis adicional con el programa Modellus, cuyo objetivo será constatar que las dos ecuaciones diferenciales (de enfriamiento y de calentamiento) y sus soluciones matemáticas concuerdan con los resultados experimentales.

 
 
 
 
 

ANÁLISIS CON MODELLUS

  
     
 

Para realizar el análisis, se incorpora a una página del programa la gráfica experimental obtenida en el estudio con los sensores.

 

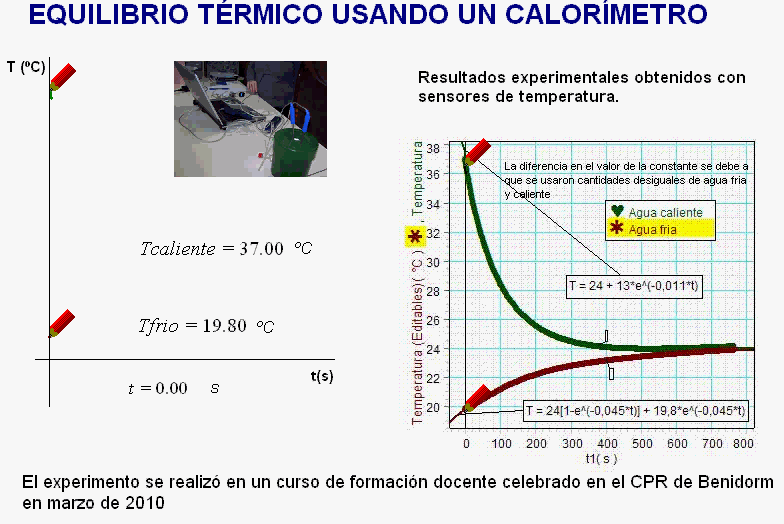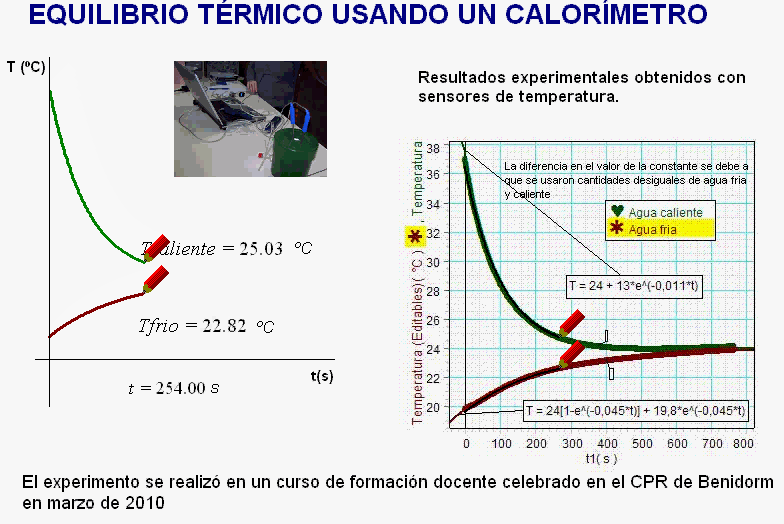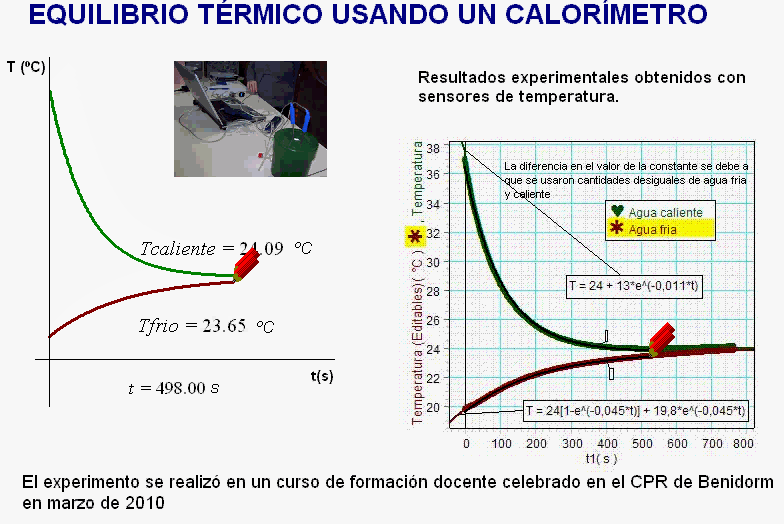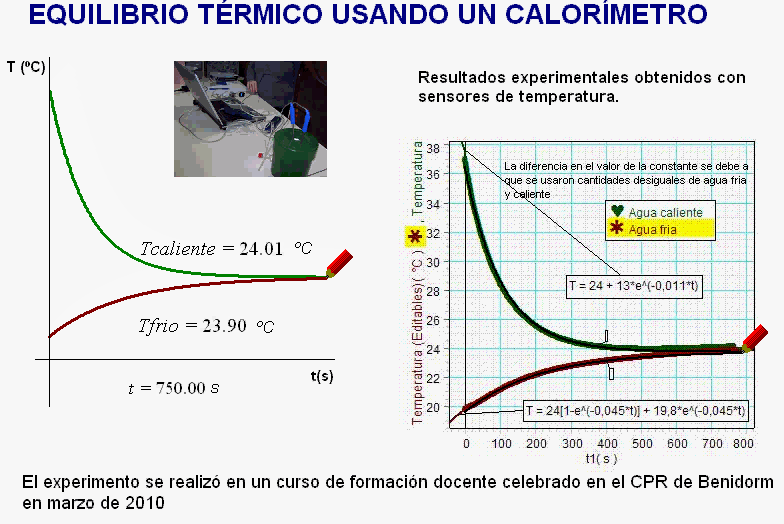
Como modelo físico-matemático de la simulación, se escriben las expresiones diferenciales que, a modo de hipótesis, plantean los alumnos para interpretar el enfriamiento [dT = -k·(T-Ta)dt] y el calentamiento [dT = k·(Ta-T)dt].

Y, se aplican los valores de las constante de enfriamiento o calentamiento, k, y el de la temperatura ambiente, Ta, obtenidos en el experimento con el sensor.

Después de aplicar la escala que da la equivalencia entre píxeles y unidades de tiempo y de temperatura, vemos que las gráficas de la simulación (de enfriamiento y de calentamiento) se superponen con una buena precisión a las gráficas experimentales.

Por tanto, se constata que las gráficas experimentales, las gráficas virtuales y la expresiones diferenciales que recogen las hipótesis concuerdan.

Clic aquí descarga la animación.