|
|
|
 |
|
EQUILIBRIO TÉRMICO DE AGUA FRÍA Y CALIENTE |
|
|
|
Experimentos realizados por
alumnos de 4º ESO en la Ikastola "Passaia-Lezo" en Guipuzcoa, y por
profesores de Física en un curso de formación docente celebrado en el
CPR de Avilés en 2010.
|
|
|
|
|
| |
|
|
| |
|
|
|
TEMPERATURA Y EQUILIBRIO TÉRMICO |
| |
|
|
|
Según el
modelo
cinético-corpuscular de la materia la
temperatura de un cuerpo es proporcional a la energía cinética
media de sus partículas, con independencia de
que dichas partículas se muevan libremente
(gas), lo hagan formando grupos variables (líquido) o
vibrando alrededor de unas posiciones fijas (sólido).
|
| |
|
 |
|
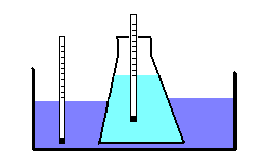
Una consecuencia de
este concepto es la evolución de la
temperatura de los sistemas hacia un equilibrio térmico con
los que les rodean. Por ejemplo, en la
situación que ilustra la figura adjunta,
las moléculas del líquido encerrado en
el matraz golpean a las del vidrio de
dicho recipiente y éstas golpean a las del
líquido del exterior. Suponiendo que la
temperatura inicial de ambos líquidos
sea diferente, estas interacciones provocan que la
temperatura del líquido que estaba más
frío aumente paulatinamente y la del que
de inicio estaba más caliente disminuya.
El proceso tiende a una situación final
de equilibrio térmico entre ambos
líquidos y con el vidrio del matraz (y,
también desde luego, con los
termómetros). |
|
|
|
|
| |
|
| |
|
 |
| |
|
HIPÓTESIS SOBRE EL ENFRIAMIENTO Y SOBRE EL
CALENTAMIENTO |
| |
| |
|
 |
|
Nos planteamos el
problema de cómo evolucionará la
temperatura de un objeto, como, por
ejemplo, un pan, que se saca de un horno
caliente y se deja enfriar encima de una
mesa. Teniendo en cuenta los conceptos
vertidos en el apartado anterior acerca
del equilibrio térmico, es lógico
plantear que el descenso de temperatura, dependa
en cada instante de la diferencia entre
la temperatura actual del cuerpo, T,
y la temperatura ambiente, Ta.
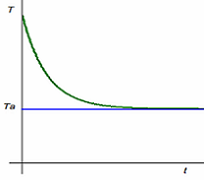
Por otro lado, puesto que durante el proceso
la temperatura, T, del cuerpo
está disminuyendo, la relación entre
dicha temperatura, T, y el
tiempo, t, no puede ser lineal,
sino que T disminuirá cada vez
más lentamente hasta alcanzar el objeto
la temperatura ambiente, Ta, tal
como indica la figura adjunta. |
|
|
|
| |
|
|
| |
|
 |
|
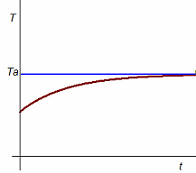
El mismo razonamiento se puede aplicar al
proceso de calentamiento de un objeto frío,
como, por ejemplo, un yogur, que se saca de un
frigorífico y se deja encima de la mesa. En este
caso, la temperatura del yogur irá aumentando
cada vez con mayor lentitud hasta que el yogur
alcance la temperatura ambiente.
Adicionalmente, en ambos casos, se espera que en
la rapidez con que se produce el enfriamiento o
el calentamiento influyan otros factores, como,
por ejemplo, la masa del cuerpo, su calor
específico, etc. |
|
|
| |
|
|
| |
Estas hipótesis indican que la
dependencia de la temperatura con el tiempo no es
lineal y se ha de usar el cálculo diferencial
para transitar desde dichas hipótesis hacia la obtención
de sendas leyes sobre el enfriamiento y sobre el
calentamiento. En el
documento vinculado se reproducen los desarrollos
correspondientes y las expresiones de dichas leyes. |
|
| |
|
|
|
|
| |
|
 |
| |
|
DISEÑO EXPERIMENTAL |
| |
| |
|
 |
|
Para estudiar el
proceso hacia el equilibrio térmico de
dos cuerpos en contacto, preparamos agua
caliente y agua fría en dos vasitos de
tamaño adecuado para ser introducidos en
un calorímetro.
Después de cerrar el
calorímetro, se introduce un sensor de
temperatura en cada vaso con agua
(caliente/fría) y se mide la evolución
de ambas temperaturas, que, según las
hipótesis que acabamos de hacer,
deberían tender a equilibrarse. |
|
|
| |
|
|
|
|
| |
|
 |
|
|
|
EQUILIBRIO TÉRMICO ENTRE AGUA CALIENTE Y
AGUA FRÍA |
| |
|
|
|
Se exponen, en primer lugar, resultados
procedentes de un experimento realizado en marzo
de 2010 en el Centro de Profesores y Recursos de
Benidorm (la sesión la impartió el profesor Vicent Soler del IES "Sixto Marco de Elche"). Los profesores usaron
agua caliente, obtenida después de
calentar agua del grifo con un mechero "Bunsen",
y agua fría, obtenida después de mezclar agua
del grifo con cubitos de hielo. Echaron
el agua fría y el agua caliente a dos
vasitos y, después de colocarlos dentro
del calorímetro, midieron la evolución
de las temperaturas. Como se observa, se
tardó algo más de 12 minutos en
alcanzar una situación de equilibrio
térmico entre ambas masas de agua. |
|
| |
|
 |
|
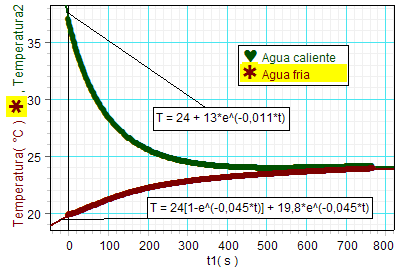
Para analizar los
datos realizamos ajustes definidos por
el usuario que aplican las leyes de
enfriamiento y calentamiento. El
resultado pone en evidencia un alto
grado de cumplimiento de los resultados
empíricos con las dos leyes:
Enfriamiento T = To
+ (Tmax-Teq)·
e-k·t
(en este caso, Teq =
24 ºC, Tcaliente = 37 ºC)
Calentamiento T = Teq
(1- e-k´·t
)+ (Tmin)·
e-k'·t
(en este caso, Teq = 24 ºC,
Tfria = 19,8 ºC)
(Las constantes
k y
k' son diferentes porque se usaron
cantidades de agua distintas) |
|
| |
|
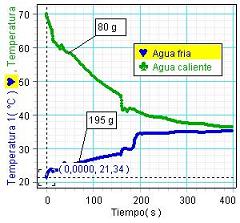
En segundo lugar, se exponen
(debajo) resultados obtenidos por el
profesor Mikel Etxaniz, de la Ikastola "Pasaia-Lezo",
en Guipuzcoa, con alumnos de 4º ESO en 2010.
Usaron el montaje de la foto, donde se introduce un vaso
de precipitados pequeño (con agua caliente) en otro vaso
mayor (con agua fría). |
| |
|
El nivel del agua
fría supera al del agua caliente, de forma que
el agua fría “rodea” el agua caliente y absorbe
la mayor parte de la energía desprendida por la
misma, minimizando la pérdida al ambiente.
Aunque proporciona resultados algo menos
precisos, este montaje tiene la virtud de
mostrar a los alumnos un “contacto directo”
entre agua caliente y fría, con lo que resulta
más intuitiva y clara para ellos la
transferencia de energía entre ambas (con el
calorímetro dicha transferencia de energía se
produce de forma indirecta, a través del aire
del interior de dicho calorímetro). |
|
 |
|
 |
|
| |
|
|
|
| |
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Puedes descargar los
resultados originales
de los tres experimentos que
se describen en esta página. Para abrir los archivos se necesita el programa DataStudio, del que tienen
licencia bastantes departamentos de Física y Química de
Institutos de Enseñanza Secundaria. |
|

