| |
|
|
| |
|
PLANTEAMIENTO
DEL EXPERIMENTO |
|
|
|
|
| |
|
|
| |
Según el
modelo
cinético-corpuscular de la materia la temperatura de un cuerpo
es proporcional a la energía cinética media de sus partículas,
con independencia de que dichas partículas se muevan libremente
(gas), lo hagan formando grupos variables (líquido) o vibrando
alrededor de unas posiciones fijas (sólido). Una consecuencia de
este concepto es la evolución de la temperatura de los sistemas
hacia un equilibrio térmico con los que les rodean, de tal forma
que en los procesos de enfriamiento, se
produce un intercambio de energía entre el ambiente (el aire del
laboratorio) y el objeto que se enfría (el agua o el sensor). El
aire del laboratorio se calienta de forma insignificante (hay
mucha mayor cantidad) y el agua o el sensor se enfría hasta
alcanzar prácticamente la temperatura inicial del aire. En
consecuencia la disminución de temperatura durante el proceso de
enfriamiento no es lineal, puesto que su ritmo depende en cada
instante de la diferencia entre la temperatura del objeto en ese
instante y la final en el equilibrio. |
|
| |
|
|
| |
Los alumnos de
Secundaria/Bachillerato pueden prever este proceso no lineal de
enfriamiento, planteando a modo de hipótesis una expresión
diferencial sobre la evolución de la temperatura del cuerpo que
se deja enfriar. No obstante, no tienen nivel suficiente de
matemáticas para resolver la ecuación. El programa Modellus
resulta muy útil para superar esta dificultad, porque permite constatar que la ecuación
diferencial y su solución matemática concuerdan con el
resultado experimental. |
|
| |
|
|
| |
|
|
| |
|
ANÁLISIS
EXPERIMENTAL CON MODELLUS |
| |
|
Para
realizar el análisis experimental, se incorpora a una página
de Modellus la gráfica experimental del proceso de enfriamiento
y, como modelo físico-matemático de la simulación, se
escribe la expresión diferencial que, a modo de
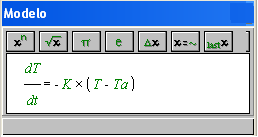
hipótesis, pueden plantear los alumnos para interpretarlo [dT = -k·(T-Ta)·dt].
En la pantalla
se añaden sendos controladores manuales que permiten modificar sobre
la marcha valor de la constante de enfriamiento
o calentamiento, k, y el de la
temperatura ambiente, Ta.
|
|
 |
|
|
|
| |
|
|
| |
 |
|
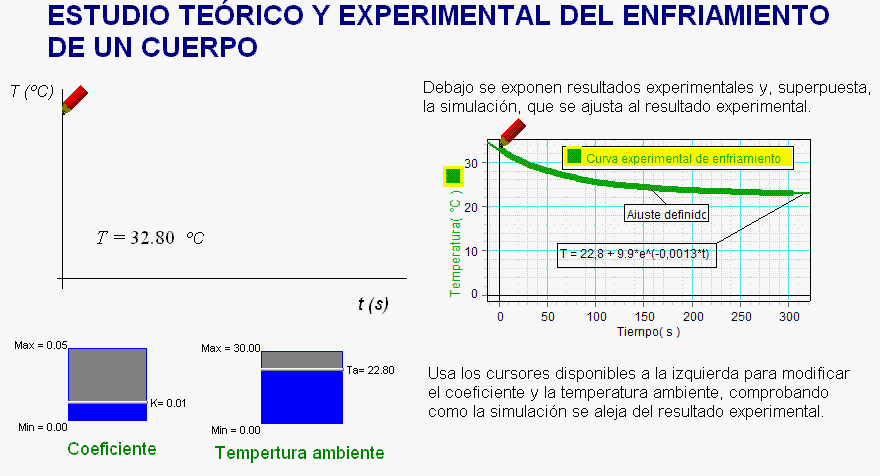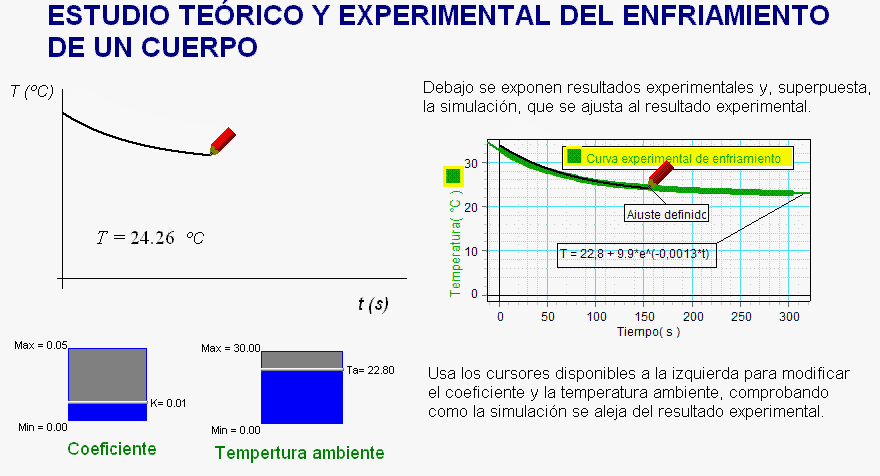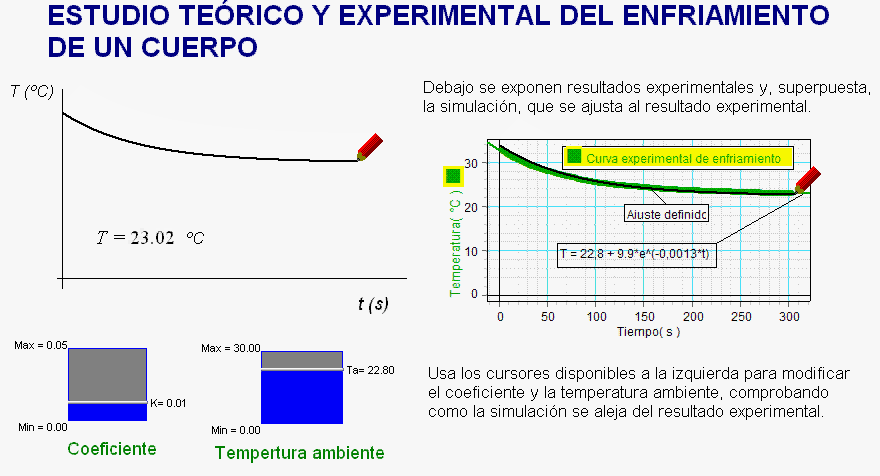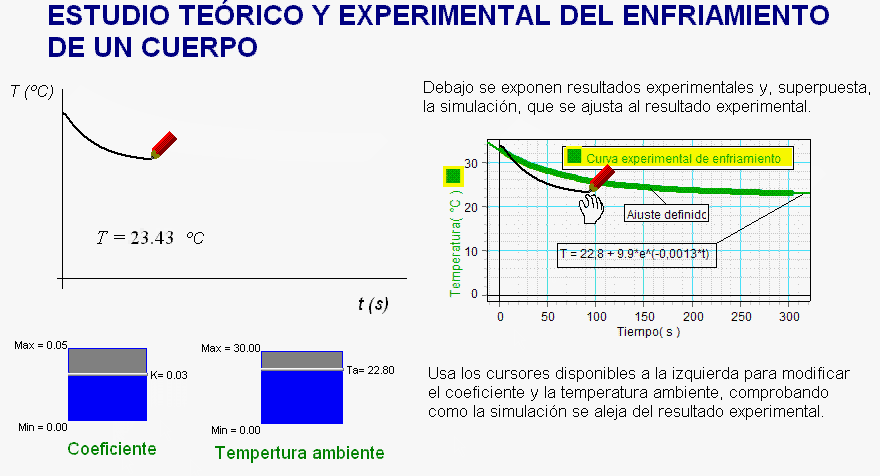
En estas
condiciones se observa (después de aplicar la escala
correcta para
establecer una equivalencia entre píxeles y
unidades de tiempo y de temperatura)
que la gráfica de la simulación se superpone con un alto grado de precisión a la gráfica
experimental, únicamente cuando se hacen
coincidir con lesos controladores los valores experimentales
(ya obtenidos en el análisis previamente
realizado con el software de los sensores) de
la temperatura ambiente (Ta) y
de la constante de enfriamiento (k).
Por tanto, se constata que la gráfica
experimental, la gráfica virtual, la expresión
diferencial y, si se quiere, también su solución
concuerdan.
Clic
aquí
descarga la animación.
|
|
|
| |
|
|
| |
|
|
| |
|
 |
|
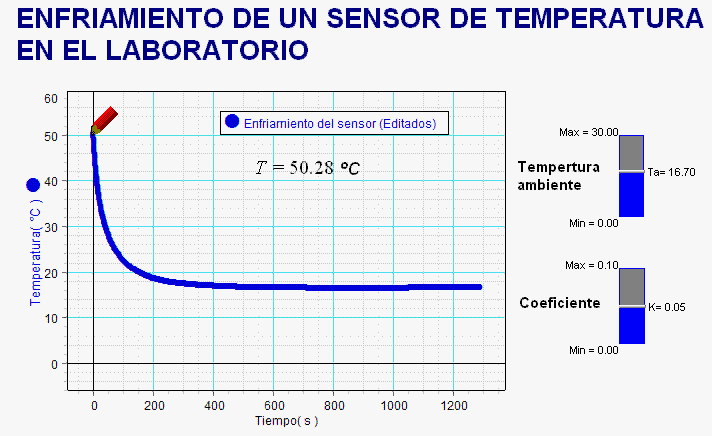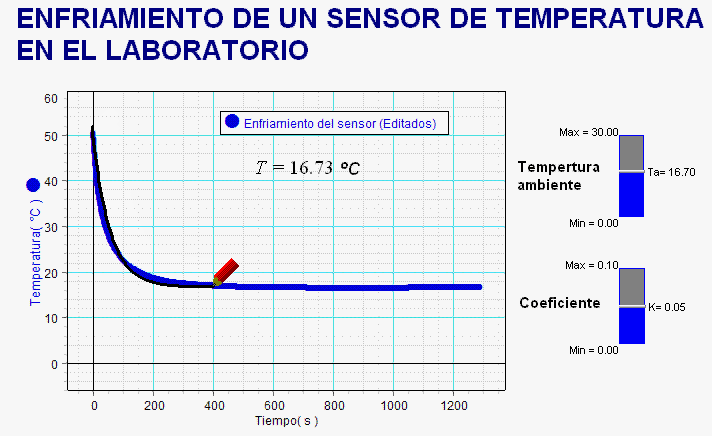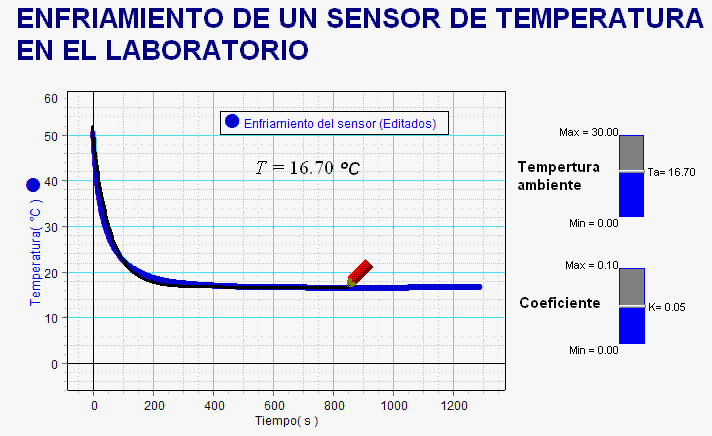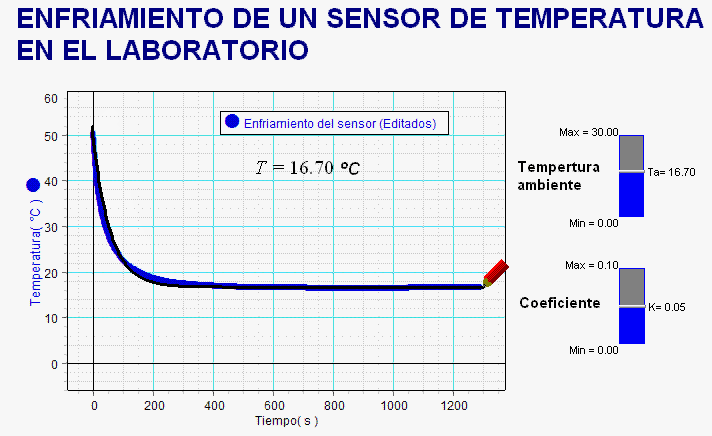
Esta otra animación
corresponde al experimento, realizado en el Instituto
por alumnos de 3º ESO en 2013 (en este caso, estudiaron
el enfriamiento del propio sensor). En este nivel,
obviamos escribir la ley matemática del proceso de
enfriamiento, pero ello no impide a los estudiantes
comprobar la concordancia entre la gráfica experimental
del proceso y la simulación, cuyo modelo
físico-matemático, recoge sus hipótesis.
Clic
aquí
descarga la animación.
|
|
|
| |
|
|
|

