|
|
|
 |
|
CURVAS DE ENFRIAMIENTO |
|
|
|
Experimento realizados por
alumnos de 3º ESO en el IES "Leonardo da Vinci" de Alicante.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HIPÓTESIS Y PROPÓSITO DEL EXPERIMENTO |
| |
| |
|
 |
|
Nos
planteamos estudiar la evolución de la temperatura de un
objeto, como, por ejemplo, una pizza,
que se saca de un horno caliente y se
deja enfriar encima de un plato. Pedimos a los estudiantes (3º ESO)
que expresen hipótesis y que
las concreten mediante una posible
gráfica (cualitativa) de la evolución
de
la temperatura con respecto al tiempo.
Aunque es evidente que ellos saben que
la temperatura disminuye
progresivamente, pueden proponer
diferentes gráficas, dependiendo del
nivel de complejidad de sus hipótesis y
de su capacidad para trasladar dicha
hipótesis a la representación. |
|
| |
|
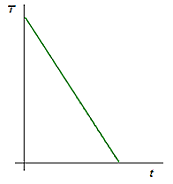
La mayoría de alumnos
predicen una disminución lineal de la
temperatura y varios de ellos además
olvidan que el enfriamiento ocurre en un
lugar, cuya temperatura ambiente está
bastante por encima de 0º (hipótesis 1,
gráfica de la izquierda).
|
| |
|
 |
|
 |
|
 |
| |
|
Varias hipótesis de los
alumnos de 3º ESO acerca del
proceso de enfriamiento |
|
|
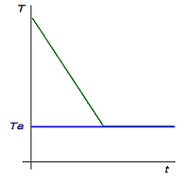
Otros coinciden con
la hipótesis de una disminución lineal
de la temperatura y sí tienen en cuenta
que la temperatura final ha de coincidir
con la temperatura ambiente (hipótesis
2, gráfica central).
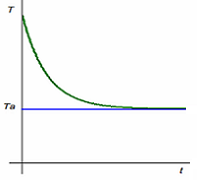
Y muy pocos tienen en cuenta que, como durante el enfriamiento
la diferencia entre la temperatura del
cuerpo y la temperatura ambiente (T-Ta)
va siendo menor a medida que el cuerpo
se enfría, la relación entre la
temperatura, T, y el tiempo, t,
no puede ser lineal, sino que
T debería disminuir cada vez más
lentamente (hipótesis
3, representada en la gráfica situada
más a la derecha).
|
|
| |
|
Probablemente, la dificultad que encuentran los
alumnos de 3º ESO para hacer esta última predicción se deba
principalmente a la propia dificultad del
razonamiento requerido, pero tampoco hay que descartar que
también influyan los resultados que han podido
obtener previamente en el
experimento sobre el calentamiento de
una masa de agua. La diferencia
fundamental entre ese proceso y el que se va a
estudiar aquí, se debe al papel que allí juega
la resistencia sumergible. En aquel experimento
la
resistencia aportaba continuamente al agua energía, mientras ella misma también se
calentaba (conectada a la red) y era este
aporte continuo de energía, lo que podía producir un
aumento lineal de la temperatura.
En cambio, en el proceso de enfriamiento que se
va a estudiar ahora, la energía se intercambia
entre el ambiente (el aire del laboratorio) y el
cuerpo. El aire se enfría (de forma
insignificante por que hay mucha mayor cantidad)
y el cuerpo se calienta (hasta alcanzar
prácticamente la temperatura inicial del aire
que apenas se enfrió). Ninguno de los dos procesos
(enfriamiento del aire y calentamiento del
cuerpo) es lineal, porque sus ritmos dependen
en cada instante de la diferencia entre la
temperatura de cada material en ese instante y la
final en el equilibrio. |
| |
|
|
|
|
| |
|
 |
| |
|
DISEÑO EXPERIMENTAL |
| |
|
|
| |
Debido a que, en principio, parece difícil
medir la temperatura de un objeto sólido los alumnos suelen
plantear que se estudie el enfriamiento de un líquido, como, por
ejemplo, una masa de agua previamente calentada en un vaso de
vidrio. |
|
| |
|
|
| |
Sin embargo, teniendo en cuenta que ellos ya
han trabajado con el sensor de temperatura, podemos recordarles
que estrictamente dicho sensor determina en cada instante la
temperatura de su extremo metálico. Sumergido, dicho extremo está en cada instante prácticamente en
equilibrio con el agua que lo circunda y, por eso, atribuimos la
temperatura que mide a la de la masa del agua. Por tanto, si
después de haber calentado el sensor, lo sacamos del agua,
también se enfriará paulatinamente hasta que alcance la
temperatura ambiente, y esto nos daría un procedimiento muy sencillo
para estudiar la evolución de la temperatura de un objeto sólido
(el propio sensor). |
|
| |
|
|
| |
|
 |
|
Teniendo en cuenta estos razonamientos
concretamos un diseño experimental muy sencillo
y adecuado para estudiar simultáneamente el
proceso de enfriamiento de una masa de líquido
(agua) y el de un cuerpo sólido (el sensor).
Para ello, primero se calentará el agua en una vaso de
precipitados, con el sensor de
temperatura y un termómetro tradicional y/o un
segundo sensor, sumergidos en él. Después se
dejará enfriar el agua y se sacará un sensor,
dejándolo enfriar, por ejemplo, encima de la
propia mesa del laboratorio.
Usando el termómetro
tradicional y/o el segundo sensor (que permanecerá
sumergido en el agua) se estudiará la evolución
de la temperatura del agua durante el proceso de
enfriamiento, mientras también se estudia
la evolución de la temperatura del segundo sensor
que se enfría al aire. |
|
|
|
|
|
|
| |
|
 |
| |
|
RESULTADOS |
| |
|
|
|
 |
|
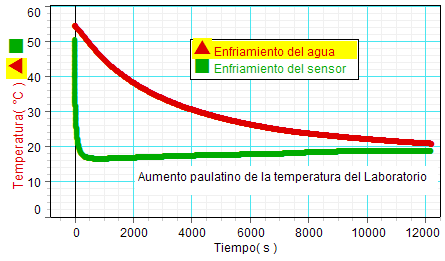
Se muestran
juntas gráficas experimentales relativas
al enfriamiento al aire del sensor y al de la
masa agua contenida en el vaso de
precipitados. Lo primero que llama la
atención es que el sensor
se enfría muy rápidamente (en unos
minutos), mientras que el agua necesita
más de tres horas para alcanzar la
temperatura del laboratorio (tras
comprobar la lentitud del enfriamiento
del agua, los alumnos dejaron
funcionando el montaje y volvieron al
laboratorio al final de la mañana).
Esta
diferencia tan acusada en el tiempo de
enfriamiento es consecuencia de que: a)
la masa de agua es mucho mayor que la
del sensor; b)
en relación con su masa, la superficie
de contacto del agua con el exterior es
mucho menor que la del sensor ; c) la mayor
parte de la superficie del agua está en
contacto con el vidrio, que lo aísla
bastante del aire (para que el agua
alcance la temperatura del laboratorio,
se tienen que el
vidrio y el agua, hasta que se alcance
el equilibrio térmico entre los tres: aire, vidrio y agua).
|
|
| |
|
En la gráfica también se observa que la
temperatura del laboratorio estuvo aumentado a
lo largo de las casi tres horas y media que duró el
experimento. Por eso, después de enfriado el sensor, la temperatura de éste, en equilibrio
térmico con el aire, también fue aumentando
paulatinamente. |
|
|
|
 |
|
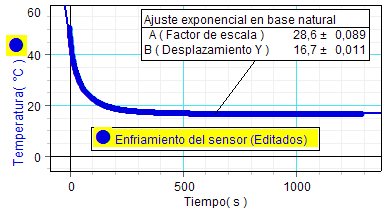
Ambas gráficas
por otra parte, confirman la hipótesis de una dependencia
no lineal de
la temperatura con el tiempo durante el enfriamiento.
Por tanto, se requiere
precisar más la hipótesis, puesto que se ha de usar el cálculo
diferencial para transitar desde las
hipótesis hacia la expresión de una
posible ley
sobre el proceso de enfriamiento. Los
estudiantes de 2º ESO no tienen un nivel
matemático suficiente para hacer esto,
pero sí podemos mostrarles que entre los
ajustes matemáticos disponibles en el
programa de análisis, uno (el ajuste
exponencial en base natural) se
acopla bastante bien a los resultados
experimentales y permite predecir
matemáticamente la temperatura del
equilibrio.
La figura adjunta muestra el
resultado obtenido al aplicar este
ajuste a la gráfica del enfriamiento del sensor (prediciendo, en este caso, una
temperatura final de 16,7 ºC). |
|
| |
|
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Puedes descargar los
resultados originales
del experimento que
se describe en esta página. Para abrirlo se necesita el programa DataStudio, del que tienen
licencia bastantes departamentos de Física y Química de
Institutos de Enseñanza Secundaria. |
|