Después de plantear hipótesis sobre el movimiento de caída libre y haber comprobado empíricamente que en ausencia de rozamiento cuerpos de masas muy diferentes caen igual, nos planteamos estudiar con detalle este movimiento intentando escribir sus ecuaciones y obtener (si el movimiento fuera uniformemente acelerado) la aceleración de caída.

Entre los diseños experimentales que proponen los estudiantes, éste montaje es el más sencillo. Se utiliza un sensor de movimiento conectado al ordenador y colocado en el suelo enfocado hacia el techo. En grupos de dos alumnos, uno deja caer un objeto sobre él y el otro trabaja  con el ordenador para tomar la lectura de las posiciones a intervalos iguales de tiempo.

La experiencia acumulada en el estudio de movimientos usando sensores de posición aconseja además que la superficie que se enfrenta al sensor sea plana y en todo momento lo más paralela posible a la superficie emisora de señales desde el sensor. Se utilizan recipientes de plástico, que se pueden enfrentar al sensor por la tapa (cara plana) y que debido a su poca masa no dañan al sensor, aunque caigan sobre él.

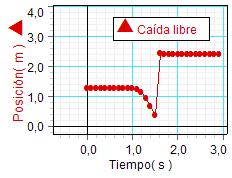
ENSAYO EXPLORATORIO: Por defecto, el sensor de movimiento trabaja a 10Hz, es decir, toma 10 imágenes por segundo. Dejando caer el objeto desde una altura moderada (entre 1 y 2 metros), sólo puede registrar 4 o 5 valores de la posición durante la caída. Resulta interesante, de todas formas, describir las gráficas obtenidas en este ensayo exploratorio: Se obtiene un buen número de valores de la posición fija que tiene el objeto antes de caer (desde que se pone en marcha el sensor hasta que empieza a caer el objeto), seguidos de 3 o 4 valores del movimiento de caída y, tras la caída, otro conjunto de valores de la posición del techo del laboratorio (hasta que se detiene el sensor).

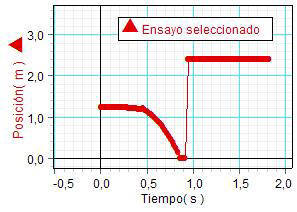
ENSAYO SELECCIONADO: Para obtener el mayor número posible de mediciones en la caída (con una imprecisión pequeña) los equipos preparan el sensor para trabajar a 50Hz. Se obtienen entonces gráficas como la mostrada, que recogen un buen número de mediciones de la posición durante la caída (hasta casi 30 mediciones) y, por lo tanto, resultan adecuadas para continuar el experimento.

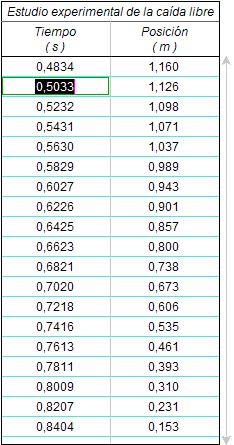
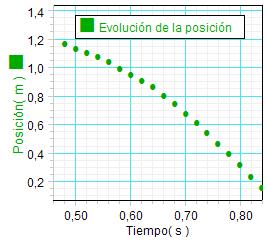
Para construir una gráfica y una tabla de valores  sobre la evolución de la posición a lo largo del tiempo, los estudiantes eliminan las mediciones que no corresponden a la caída y seleccionan un tramo de ésta. Después entran en la ventana de configuración para quitar las líneas de unión entre los puntos de la gráfica y optimizan la escala. El aspecto cualitativo de la gráfica obtenida resulta satisfactorio en relación con la hipótesis acerca del tipo de movimiento.

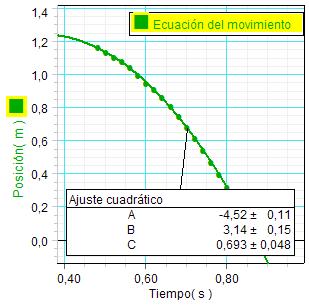
Puesto que las hipótesis emitidas en clase plantearon que el movimiento debería ser acelerado, para obtener una ecuación de la evolución de la posición interesa realizar un ajuste cuadrático. Los grupos comprueban con satisfacción que los valores experimentales se desvían muy poco de dicho ajuste.

La comparación de los resultados que proporciona el ajuste con la ecuación teórica de un movimiento uniformemente acelerado permite identificar el coeficiente A del ajuste realizado con la mitad de la aceleración.

El experimento proporcionó en este caso un valor de g igual a 9,04 m/s²

Se puede configurar desde el programa informático para que calcule directamente valores de la velocidad y la de la aceleración, pero no siempre es lo más aconsejable. Se ha de tener en cuenta que el programa obtiene estas magnitudes derivadas a partir de todos los valores experimentales de la posición y en consecuencia cada error en una medición de posiciones se traslada a las magnitudes derivadas, acumulando muchas veces imprecisiones importantes.

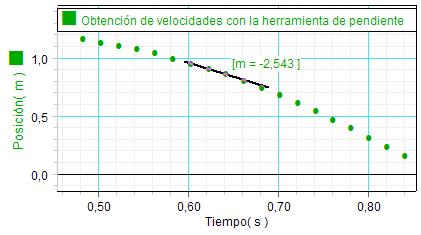
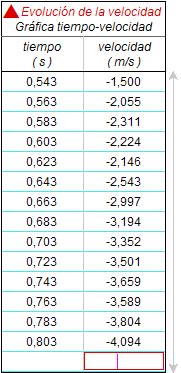
Una forma alternativa de obtener la evolución de la velocidad consiste en aplicar el concepto de que la pendiente de la gráfica tiempo-posición es la velocidad instantánea en cada punto. Manejando la herramienta de pendiente del programa (arriba) los alumnos pueden obtener los valores de la velocidad para las mediciones seleccionadas, al tiempo que repasan este concepto. Esto les permite construir una tabla de valores experimentales de la  evolución de la velocidad (derecha).

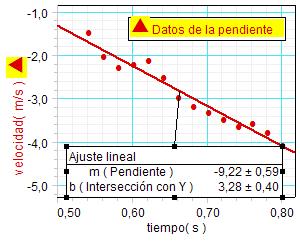
Con estos valores de la tabla tiempo-velocidad, construyen la gráfica correspondiente y realizan un ajuste lineal, puesto que, de acuerdo con las hipótesis, la ecuación de la velocidad de caída debe ser del tipo: v = - g·t.

Como se observa, en este caso, el análisis proporcionó una aceleración de caída g = 9.22 m/s². La diferencia entre este valor y el obtenido después de realizar el ajuste cuadrático en la gráfica tiempo-posición se debe a que para construir la gráfica de la velocidad se seleccionaron algunos de los valores de la pendiente de la gráfica de la posición. Interesa fijarse particularmente en que los valores seleccionados corresponden a un tramo inicial (más corto) de la caída.

Durante los cursos 2006 hasta 2010 realizaron este trabajo práctico un total de 26 grupos de alumnos y cada grupo repitió como mínimo dos veces el experimento. Los valores de g obtenidos oscilaron entre un valor mínimo de 7,8 m/s²  y el valor máximo de 9,22 m/s², que recogemos aquí. El margen de error de los sensores se puede estimar en un 10%, de modo que no debería de pasar desapercibido el hecho de que todos los resultados experimentales obtienen una aceleración de caída inferior a su valor teórico (9,83m/s²), en ausencia de rozamiento. Este hecho sugiere que la influencia del rozamiento sobre el movimiento de caída de los objetos de plástico utilizados es significativa, incluso para una altura tan pequeña.

Se plantea, en consecuencia, una necesidad de ampliar la investigación para estudiar la influencia del rozamiento del aire en la caída y, por otra parte, disminuir dicha influencia todo lo posible.

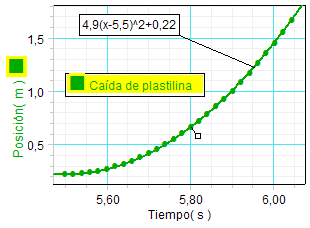En este caso, se colocó el sensor de movimiento en el techo (la plastilina lo dañaría si cayera sobre él) y se comprobó que dicho el sensor obtiene valores precisos de las posiciones del pedazo de plastilina durante un tiempo máximo de 1,7s. Este intervalo de tiempo es más que suficiente para obtener un excelente valor de la aceleración con los datos experimentales correspondientes al tramo inicial de la caída (la gráfica adjunta se refiere a los primeros 0.6s). Este análisis ofrece otra aportación muy interesante, como es haber utilizado la opción de realizar un ajuste definido por el usuario para estudiar la gráfica. Como se observa al realizar este ajuste personal, escribimos la ecuación completa del movimiento, teniendo en cuenta que en este caso son conocidas (a través de la propia gráfica) en el instante inicial  de la caída (5.5s), la posición inicial (0.22m) y la velocidad inicial (nula).    

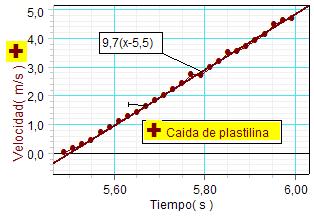
El conocimiento por este procedimiento de las condiciones iniciales del movimiento permite también realizar otro ajuste definido por el usuario sobre la gráfica tiempo-velocidad que proporciona el programa. Como se observa, el ajuste definido por el usuario se corresponde en este caso con un valor de g de 9.7 m/s².