| |
|
 |
|
CAÍDA DE UNA BOLA DENTRO DEL AGUA
2 (ANÁLISIS CON TRACKER) |
|
|
|
Experimento
realizado en 2019 en el Cefire Específico de Ciencias, Tecnología y
Matemáticas de Valencia. |
|
|
| |
|
PLANTEAMIENTO DEL EXPERIMENTO |
|
|
|
En el
experimento sobre la caída de
una bola dentro del agua realizado con Modellus, se ha
podido comprobar que
dicha bola (cuya densidad era sólo un poco mayor que la del
agua) alcanzaba enseguida la velocidad límite y
tenía, en consecuencia, un movimiento de caída prácticamente
uniforme. Nos proponemos realizar un estudio similar
usando el programa Tracker, pero ahora, extendiendo el análisis al
movimiento completo. |
| |
|
|
|
|
VIDEO DE LA CAÍDA DE LA BOLA |
|
|
|
El clip de
video adjunto muestra el movimiento
completo de
caída de la bola desde que se suelta
dentro de una probeta llena de agua. Se observa a
simple vista que, tal como prevé nuestra
hipótesis, se pueden considerar dos etapas completamente
diferenciadas en el movimiento.
- La
primera corresponde al movimiento que
comienza justo después
de que se deja caer la bola dentro del
agua y termina justo antes de que dicha
bola sufra una fuerte sacudida, que es
muy evidente
visualmente. Cabe esperar que esta parte inicial
de del movimiento de caída de la bola
sea acelerada.
- La
segunda etapa corresponde al movimiento que
comienza justo después de que la bola
sufre la
sacudida. Se observa perfectamente que
esta sacudida produce un cambio brusco
en el
movimiento de caída, y nuestra hipótesis
prevé a partir de aquí, este movimiento
será uniforme, a
la velocidad límite.
Una vez
observado y filmado el movimiento, nos
proponemos realizar un
análisis experimental de sus dos etapas, con ayuda del programa
Tracker. Para ello, como vemos en
la imagen,
el diseño experimental incluyó la
determinación de una longitud de
referencia visible a la cámara (en
este caso fue la altura de 15 cm,
convenientemente señalada al fondo de la
imagen).
Disponer de esta longitud de referencia
es imprescindible para
escribir en el programa las
ecuaciones (cuantitativas) de los dos movimientos, ya
descritos.
|
|
|
|
|
| |
|
RESULTADOS DEL ANÁLISIS
EXPERIMENTAL |
|
|
|
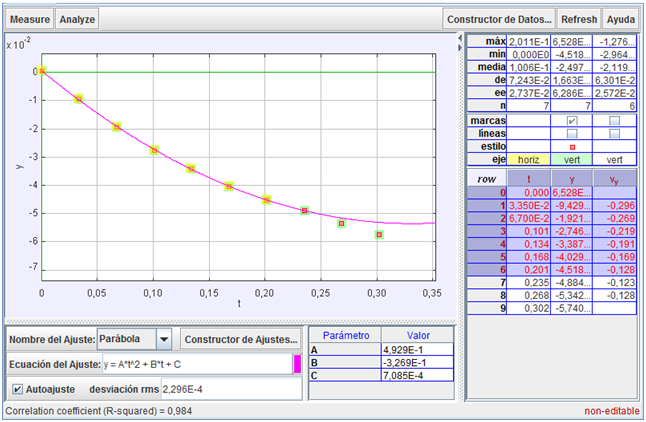
Para contrastar la
hipótesis concerniente a la primera etapa del
movimiento con la ayuda del programa
Tracker, empezamos realizando un
ajuste cuadrático de la gráfica de la posición (y = A·t2
+ B·t + C), ya que se quiere
comprobar si el tramo inicial del
movimiento de caída de la bola, sumergida en la
probeta, es acelerado. |
|
|
|
Como se observa
tras
analizar, tanto el aspecto de la gráfica, como
los valores numéricos de los diversos
parámetros, dicho ajuste (en el que, como vemos,
no se incluyeron los dos últimos puntos de la
gráfica) confirmó la
hipótesis, pudiendo afirmarse que el movimiento
de caída de la bola en su tramo inicial fue
uniformemente acelerado.
Además, sirvió para
obtener el valor de la aceleración
(prácticamente constante) de esta primera parte
del movimiento (en este caso resultó: a =
- 0,098 6 m/s, es decir, el doble del
coeficiente A, del ajuste). |
|
 |
|
| |
|
Para completar esta parte
del estudio también se representó y analizó con el
programa la evolución de la velocidad vertical de la
bola. produjeron unos resultados coherentes con los
recién comentados relativos al estudio de la evolución
de la posición |
| |
|
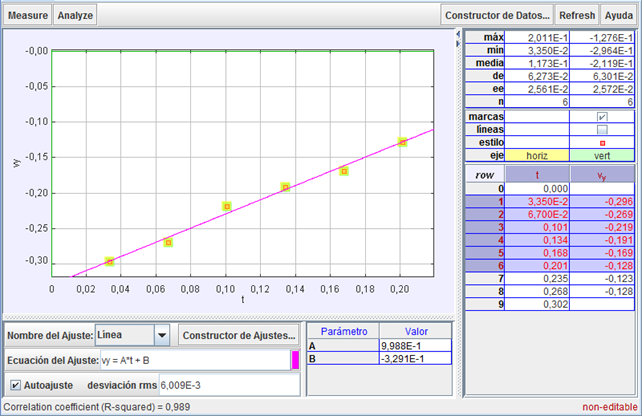
La gráfica adjunta
muestra dicha representación y dicho análisis.
Como puede verse, la relación entre el módulo de
la velocidad del movimiento inicial de caída de
la bola y el tiempo, se ajustó muy bien mediante
una expresión lineal (vy = A·t + B)
o, lo que es lo mismo, se constató que la
ecuación de la velocidad (vertical) del
movimiento de caída de la bola fue también la de
un movimiento uniformemente acelerado.
Obsérvese, por otra
parte, que el valor así obtenido del módulo de
la aceleración (a = 0,0998 m/s) apenas
difirió del obtenido en el análisis anterior.
|
|
 |
|
| |
|
Tras estos análisis
concernientes a la primera parte del movimiento, se
procedió a realizar otro análisis similar respecto del
movimiento que tiene la bola después de haber frenado
bruscamente. |
| |
|
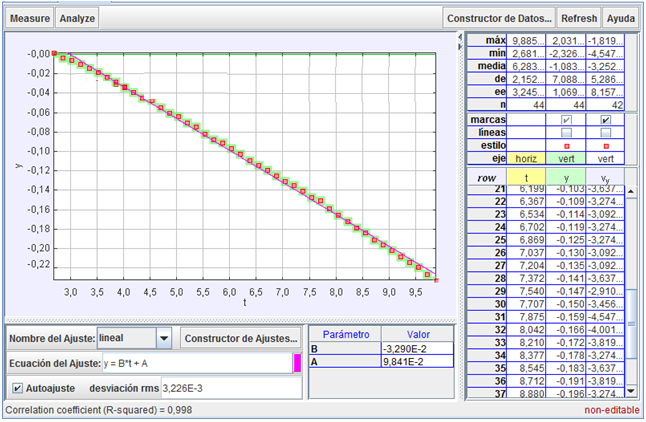
Como vemos a través
de la gráfica adjunta, en esta segunda etapa el
movimiento resulta, tal como previó la
hipótesis, prácticamente uniforme.
Así, los
valores experimentales de la posición (vertical)
frente al tiempo se ajustan perfectamente
mediante una relación lineal (y = B·t + A),
donde el coeficiente B representa la velocidad
constante de caída, igual a la velocidad límite.
Como se observa, en
este caso, dicha velocidad resultó igual a - 0,032 9 m/s.
Clic
aquí
para descargar el archivo Tracker de estos
análisis |
|
 |
|
|
|
|
|