|
|
| |
|
|
|
Del mismo modo que cuando se trabaja
con Modellus, para realizar análisis
de un movimiento con
Tracker, se empieza filmando un video del
mismo. En este caso se eligió dejar caer una
pelota de frontenis desde una altura aproximada
de un metro. Ahora bien, antes de proceder a
realizar dicha filmación hay que preparar el escenario,
conformando un montaje adecuado. Así vemos que, en
este caso, como la de frontenis es de color amarillo, se preparó un
fondo de color verde, con objeto de mejorar su
visibilidad. Por otra parte, se colocó en dirección vertical
una regla de longitud conocida, (en este caso,
de 1 m), para calibrar las distancias.
Con respecto a la
metodología a seguir para la filmación, en este
caso es importante tener en cuenta que se ha de
grabar el clip de video, procurando que la
cámara permanezca estática durante la filmación
y que lo haga en una posición lo más alineada
posible con la trayectoria de la pelota para
minimizar los errores de paralaje.
Además de todo esto
hay que registrar algunos datos, que necesarios
para programar el análisis experimental.
Concretamente es preciso conocer la frecuencia
de grabación (en este caso fue de 20 fotogramas
por segundo, es decir, transcurrían 0,05 s entre
fotograma y fotograma) y también establecer una referencia y
un criterio de signos para las magnitudes (como
se ve, en este caso se adoptó el origen en la
posición de salida de la pelota y se consideró
el eje vertical con sentido positivo en la
dirección (descendente) del movimiento.
|
|
 |
|
|
| |
|
RESULTADOS
DEL ANÁLISIS
EXPERIMENTAL |
|
|
|
 |
|
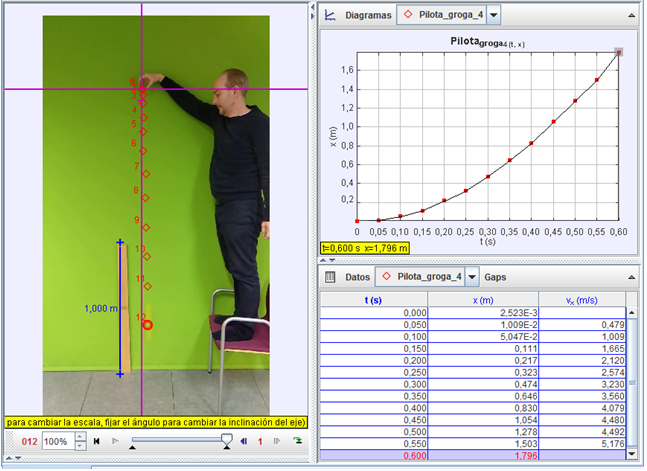
La imagen adjunta muestra
el cuadro de Tracker con el análisis de la caída, que
registra las posiciones sucesivas de la pelota
registradas cada 0,05 s.
A la derecha, en la parte
inferior, vemos la tabla de las magnitudes cinemáticas
(tiempo, posición y velocidad), y, encima de dicha
tabla, la gráfica de la posición en función del tiempo.
Cualitativamente, esta
gráfica confirma la evidencia de que el movimiento es
acelerado y, por tanto, procede realizar los ajustes
necesarios para contrastar si es, como se prevé, es
uniformemente acelerado, para obtener la aceleración y,
finalmente, para escribir las ecuaciones (cuantitativas)
del movimiento. |
|
|
|
|
|
 |
|
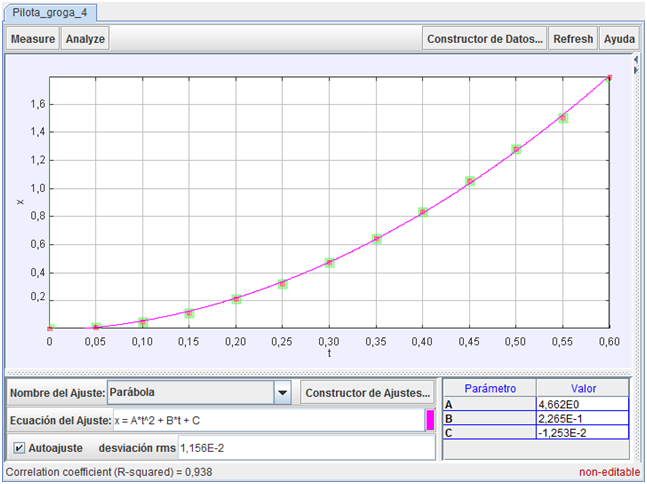
Por lo que se refiere a la
ecuación de la posición, vemos en la imagen adjunta que
la ecuación de ajuste fue la de un movimiento
uniformemente acelerado, es decir, del tipo: y = A·t2 +
B·t + C.
En esta ecuación, el valor
del parámetro C es muy próximo a cero, lo que es
coherente con el hecho de que en t = 0 s, tal comos e
adoptó el sistema de referencia, la pelota comienza su
movimiento de caída desde el origen.
En cuanto a la aceleración,
su módulo vale 9,324 m/s. es un valor próximo al
valor teórico de g (su desviación con respecto a g, es
decir, respecto a 9,8 m/s es menor de un 6 %),
aunque algo inferior.
Entre las posibles causas
de esta discrepancia en la determinación del valor de g,
hay que considerar principalmente dos tipos de ellas:
|
|
|
|
|
a) Errores de
medición diversos cometidos en alguno de los diferentes
procesos involucrados en el experimento: al calibrar la
imagen, al puntear la posición, en la misma toma del
video (posible error de paralaje debido a una colocación
no totalmente alineada con la trayectoria), etc.
b) El efecto de la
fricción del aire, que cabe suponer que no sea
totalmente despreciable, sino que provoque una
disminución progresiva de la aceleración. En el cómputo
global esto implica obtener, como así fue en este caso,
un valor menor de la aceleración aplicable a todo el
movimiento. Hay que tener en cuenta que aceleración
inicial ha de ser de unos 10 m/s2. En
consecuencia, la pelota alcanza enseguida una velocidad
importante y esto aumenta a su vez de forma importante
la intensidad de la fuerza de rozamiento (la fuerza de
rozamiento a la penetración de un sólido dentro de un
fluido aumenta de forma considerable con la velocidad) |
|
|
|
 |
|
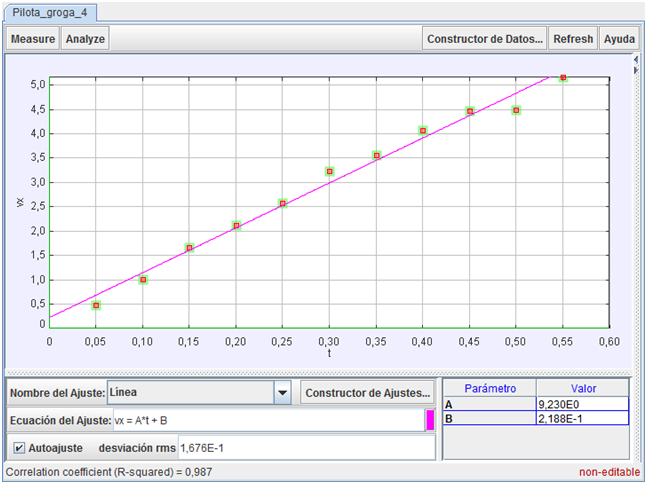
Complementariamente al
estudio de la gráfica de la posición, también es
interesante hacer un análisis similar acerca de la
velocidad.
El ajuste idóneo en este caso es lineal, es
decir, que la ecuación de ajuste (o ecuación de la
velocidad del movimiento) es del tipo: v = A·t +B. En esta
ocasión, el parámetro
A representa directamente a la aceleración, y, como
vemos, esto produce un valor de su módulo igual a
9.23 m/s2.
La pequeña diferencia entre los
valores de la aceleración que se obtienen con uno y otro
procedimientos, se debe a cómo calcula el programa cada
velocidad instantánea a partir de los datos de las
posiciones, que son los únicos datos fuente.
Clic
aquí
descarga el archivo de los análisis |
|
|
|
|
|
|