|
|
|
 |
|
EL
PROCESO DE MEDIDA |
|
|
| Experimentos
realizados por alumnos de Secundaria en el IES "Leonardo Da Vinci" de Alicante
|
|
| |
| |
 |
RECOGIDA DE UN
CONJUNTO DE MEDICIONES |
 |
IMPRECISIÓN DE LAS
MEDIDAS |
 |
VALOR REPRESENTATIVO |
 |
RUEDA DE INSTRUMENTOS
TRADICIONALES |
 |
MEDIDAS CON SENSORES |
 |
ESTIMACIONES Y
MEDIDAS |
 |
DOCUMENTOS, ARCHIVOS Y PROGRAMA
DE ACTIVIDADES |
|
|
|
|
|
|
|
|
|
|
|
RECOGIDA DE UN CONJUNTO DE MEDICIONES |
| |
| |
|
 |
|
Con objeto de tomar
conciencia de algunas dificultades que
se pueden presentar en los procesos de
medida, todos los alumnos miden la
altura de un compañero usando una cinta métrica. Cada uno realiza
la medida independientemente, y, sin
decir a nadie el valor medido, lo anota
en un papel.
Cuando todos han terminado se realiza
una puesta en común de los valores
obtenidos.
En la actividad los estudiantes
normalmente se sorprenden por obtener una serie de
valores dispersos de la altura del
compañero, lo que nos permite aclarar
que el proceso de medida lleva siempre
inherente un margen de imprecisión y que
es preciso repetir varias veces cada
medida, antes de obtener un valor
representativo. De entrada sugieren dos
posibilidades para obtener dicho valor
representativo: la moda (valor que más
se repite) y/o la media (aritmética).
Se requiere un
análisis de los resultados
y establecer criterios adecuados para
decidir entre estas dos opciones u otras
que cabe considerar.
|
|
| |
|
 |
|
|
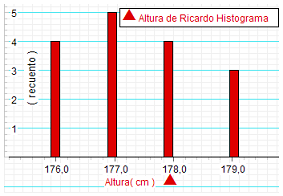
Si no se han
cometido errores graves en la
forma de medir, dicho análisis
puede comenzar representando los
resultados en un histograma y en
una gráfica ordinaria (en este
caso, los alumnos aprendieron
realizar ambas con el programa
DataStudio). |
| |
|
 |
|
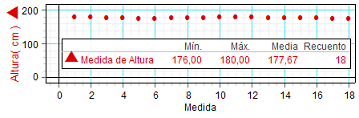
El
histograma muestra en
qué grado los valores
se distribuyen alrededor
de un "valor central", y
sobre la gráfica
ordinaria se puede
realizar una estadística
básica, calculando el
valor medio de la altura, el valor mínimo y el
valor máximo. |
|
|
|
| |
|
|
|
|
| |
|
 |
| |
|
IMPRECISIÓN DE LAS MEDIDAS |
| |
|
|
| |
Al analizar los resultados de la
altura del estudiante, se advierte que es necesario establecer
un intervalo de seguridad en torno al valor representativo de
cada medida. |
|
| |
|
|
| |
|
 |
|
Dicho
intervalo de seguridad no puede ser menor que la
sensibilidad del instrumento utilizado (en ese
caso, 0,1 cm). Para poder adoptar tal
imprecisión usando la cinta métrica se debería
haber usado un procedimiento de medida bastante
riguroso, tomando precauciones adecuadas para asegurar que las
divisiones de la escala enrasan lo mejor posible
con el extremo de la longitud medida (por
ejemplo, se puede usar un libro para marcar
previamente sobre una pared una línea que
indique la altura). |
|
|
|
|
Como las mediciones se tomaron
simplemente colocando la cinta métrica en paralelo al
estudiante medido, los propios alumnos las
expresaron directamente en cm, por tanto, atribuyéndolas una
imprecisión de 1 cm. Esta opción es menos
precisa, pero se puede considerar correcta y nos permite
poner otros ejemplos de mediciones a las que es preciso
atribuir una imprecisión mayor que la sensibilidad del
aparato. Por ejemplo, cuando medimos tiempos con un
cronómetro, cuya escala puede indicar centésimas o
milésimas de segundo, debemos tener en cuenta que por el
hecho de manejarlo manualmente, aportamos a las medidas
una imprecisión del orden de 1 s. |
|
|
|
|
|
| |
|
 |
| |
|
VALOR REPRESENTATIVO |
| |
| |
|
De los análisis
realizados se derivan varias posibilidades para
obtener el valor representativo: el valor que más se
repite (moda), el valor medio (media aritmética),
el valor central de todos después de haberlos ordenado de
menor a mayor (mediana). Estos valores pueden o no
coincidir y, en general, conviene adoptar uno
u otro como valor representativo,
dependiendo de factores como el número de
medidas que se hayan realizado (por ejemplo, no cabe hacer
la media cuando una medida se repite un número
pequeño de veces), de su dispersión (por ejemplo,
si una medición se separa significativamente del
resto cabe eliminarla del análisis), de la forma
cómo se distribuyen, etc.
En este caso, el valor que
más se repite (177 cm) coincide con la mediana,
pero es inferior a la media (178 cm; valor
redondeado para tener en cuenta la imprecisión
del instrumento). Por otra parte, la moda
(177 cm) no quedó perfectamente centrada en el
histograma, sino ligeramente desplazada hacia
los valores inferiores. Y los dos valores
representativos posibles (177 cm y 178 cm) están
rodeados de resultados experimentales mayores y
menores que ellos. El hecho de que coincidan
moda y mediana y que dicho valor quede algo más
centrado, decanta a su favor la balanza, con lo
que el valor representativo queda expresado así:
Altura del alumno: 177 cm
Imprecisión absoluta: 1 cm
Imprecisión relativa: 0,6 %
A = (177 ± 1) cm |
| |
|
|
|
|
| |
|
 |
| |
|
RUEDA DE
INSTRUMENTOS TRADICIONALES |
| |
|
|
| |
|
La realización de medidas requiere el
uso de instrumentos con los que es conveniente
familiarizarse. Con los conceptos adquiridos en las
actividades anteriores en la mano, los estudiantes
realizan una rueda de medidas usando algunos
instrumentos tradicionales. Tienen que
apuntar en el cuaderno las características básicas de cada instrumento
(magnitud que mide, escala, sensibilidad, posible error
de cero, manejo, etc.), realizar con él una medición y expresar el
resultado correctamente. |
|
|
|
|
|
|
|
|
|
| |
|
 |
| |
|
MEDICIONES CON SENSORES |
| |
|
|
| |
|
Tras la rueda de instrumentos
"tradicionales", los estudiantes realizan algunas
medidas similares usando sensores (de posición,
temperatura, fuerza, etc.). Se familiarizan con el
software requerido y, en cada caso, reflexionan sobre el
margen de imprecisión que conviene atribuir al valor
representativo. Los sensores permiten tomar en un
instante un número muy alto de mediciones,
normalmente de alta precisión. Por tanto, si la
dispersión de las medidas es pequeña, se puede adoptar
la media como valor representativo. |
|
|
|
Altura del
techo del laboratorio (sensor de posición) |
|
|
|
Para determinar la distancia a un
objeto, el sensor de posición lanza un haz cónico de
luz y mide el tiempo que tarda dicho haz en ir, ser
reflejado por la superficie del objeto, y volver.
Sabiendo esto se comprende que, para optimizar la bondad
de la medida de la distancia entre el sensor y un objeto
en reposo (en este caso, el techo del laboratorio),
interesa configurar el instrumento para que trabaje a la
menor frecuencia. Así se evitan posibles
interferencias entre haces sucesivos, que pueden
producir imprecisiones. |
|
|
|
 |
|
|
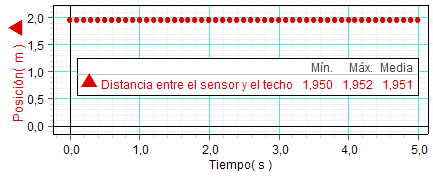
En el ejemplo
adjunto, se observa que la desviación de
las medidas fue pequeñísima. Por tanto,
se puede dar el siguiente resultado
de la medición: |
| |
|
Distancia entre el sensor (colocado en
el suelo) y el techo =
(1,952 ± 0,001) m |
| |
|
Ahora bien, para
obtener la altura del techo (medida
desde el suelo) hay que
sumar a esta distancia la del propio sensor, que también debe ser medida, lo
que condiciona a la imprecisión del
resultado final (explicamos a los
alumnos que se debe adoptar la mayor
entre las dos medidas efectuadas).
|
|
|
|
|
|
|
|
|
Temperatura del laboratorio (sensor de
temperatura) |
|
|
|
Aún usándose a la menor frecuencia
(10 Hz) el sensor de temperatura obtiene en un tiempo muy
corto un número elevado de valores, generalmente poco
dispersos, y con precisión de una centésima de grado centígrado. |
|
|
|
 |
|
|
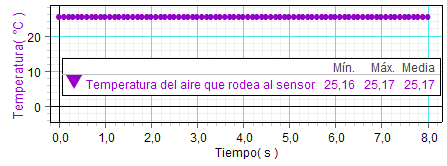
En el ejemplo
adjunto, cabe adoptar el siguiente valor
representativo: |
| |
|
Temperatura del aire que rodea al sensor =
(25,17 ± 0,01) ºC |
| |
|
Estrictamente, la
temperatura obtenida es la del aire que
rodea al sensor. Se puede dar un valor
medio de la temperatura del
laboratorio, a partir de los
valores que obtienen en sus zonas
respectivas varios grupos de alumnos
(en este caso, la dispersión entre las
medidas de 4
grupos fue tan sólo de 0,01 ºC) |
|
|
|
|
|
Ya se comprende que la diferencia
entre este valor de la temperatura y el obtenido con el
termómetro de pared es debida simplemente a que las
mediciones se realizaron dos días diferentes. |
|
|
|
|
|
|
|
|
 |
| |
|
ESTIMACIONES Y
MEDIDAS |
| |
|
|
| |
|
Además de medir
correctamente es muy importante hacerse una idea previa aproximada del orden de
magnitud de las mediciones. Con este objetivo los
estudiantes realizan algunas
estimaciones de cantidades cotidianas (la masa de un
estuche lleno de lápices, el volumen de agua que hay en
un vaso, la altura de una mesa) y luego las miden,
para comprobar si su estimación fue correcta. |
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
DOCUMENTOS, EJERCICIOS Y
PROGRAMA DE ACTIVIDADES |
|
 |
PROGRAMA DE ACTIVIDADES: Programa-guía con las actividades
usadas para realizar en el laboratorio estos trabajos prácticos
y algunos ejercicios complementarios. |
|
 |
NORMAS PARA REALIZACIÓN DE
MEDIDAS: Listado
de normas para realizar mediciones en el laboratorio de Física. |
|
 |
FICHA:
Modelo de ficha para dar
características de un instrumento de medida. |
|
 |
SISTEMA
INTERNACIONAL DE UNIDADES:
Real Decreto 493/2020, de 29 de abril, por el que se
establecen las unidades legales de medida. |
|
 |
ARCHIVOS DE
DATASTUDIO:
Archivo del análisis de todas las mediciones realizado con el programa DataStudio. |
|
|
|
|
 |
