| |
|
|
|
|
PROPÓSITO DEL
EXPERIMENTO |
| |
|
En el estudio del péndulo
simple realizado con Modellus, hemos visto que el
movimiento real del péndulo y un movimiento teórico
simulado, concuerdan para un valor de la aceleración de
la gravedad, g, del orden de 9,83
m/s2.
Aquí nos proponemos realizar un
estudio similar usando el programa Tracker, con
el que, además de estudiar esta esperada concordancia,
realizaremos algunos también análisis cuantitativos
sobre la evolución de las magnitudes que describen
al movimiento del péndulo simple.
|
|
| |
|
MONTAJE EXPERIMENTAL.
VIDEO DEL MOVIMIENTO DE OSCILACIÓN DEL PÉNDULO |
| |
|
Para este estudio se montó
un péndulo con un apoyo vertical, un hilo de poca masa e
inextensible y una esfera de material denso (m = 53,24 g).
La longitud del péndulo fue 96,5 cm y junto a él, se
colocó, como vemos, una regla (de 1 m de longitud) para
calibrar la imagen en la pantalla. |
| |
|
Después de desplazar
ligeramente la esfera de la posición vertical y soltarla
para generar oscilaciones de pequeña amplitud, se filmó
el movimiento. |
| |
|
Seguidamente se realizó un
análisis previo de las imágenes con el propio programa
Tracker, con objeto de seleccionar un intervalo de
tiempo en el que se observaron las oscilaciones más
simétricas.
Finalmente, se realizó la conversión entre
píxeles y metros (usando como dato de referencia la
longitud de la regla) y se escribió el modelo
físico-matemático de la simulación (conformado por las
ecuaciones teóricas del movimiento de oscilación del
péndulo simple, cuyos parámetros coincidan con los
valores del caso real) |
|
|
|
|
|
|
ANÁLISIS
EXPERIMENTAL CON TRACKER |
| |
|
Tras llevar
adelante estos procesos, se realizaron diversos
análisis, obteniendo, entre otros, los siguientes
resultados: |
| |
|
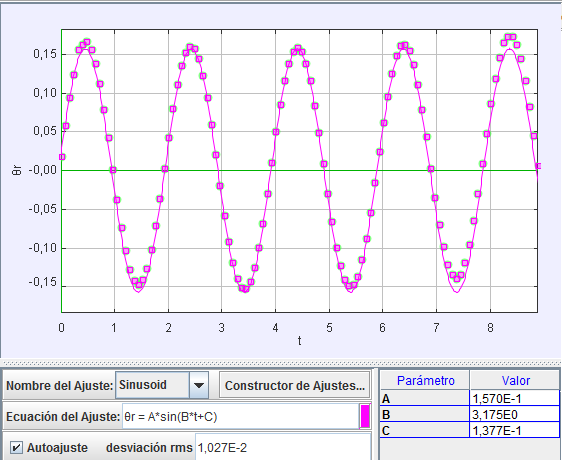
Gráfica del movimiento |
| |
|
Esta representación puede
servir para mostrar a los alumnos que
usando magnitudes angulares para
expresar la posición del péndulo (en
este caso, el ángulo en radianes), la
gráfica del movimiento es similar a la
que podría obtener usando magnitudes
lineales (la posición expresada, por
ejemplo, en centímetros)
|
|
 |
|
| |
|
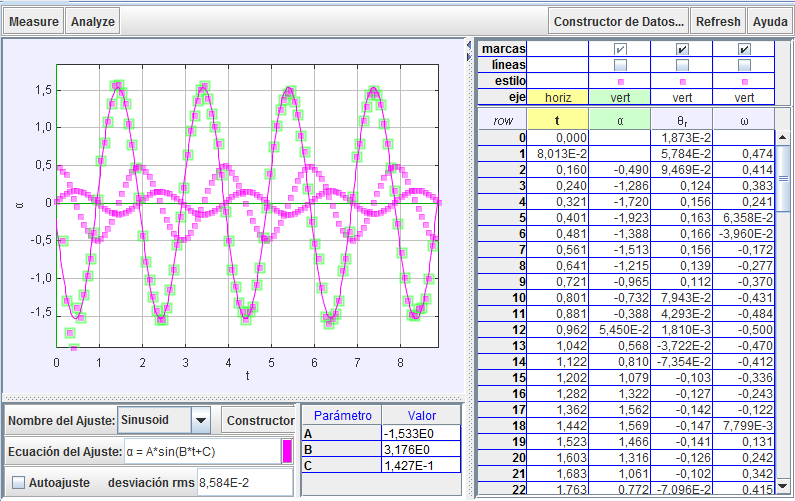
Gráficas de la
posición, velocidad y aceleración angular |
| |
|
En la gráfica adjunta se representan el
ángulo θ respecto de la vertical (rad), la velocidad
angular w (rad/s) y la aceleración angular α (rad/s2).
Los puntos experimentales ajustados a la función
matemática sinusoidal corresponden a los valores de
aceleración angular (sombreados en verde).
Es muy útil
incorporar en la misma representación a las tres
magnitudes (posición, velocidad y aceleración angular),
para que los estudiantes comprueben los desfases
existentes entre ellas (por ejemplo, cuando el péndulo
pasa por la posición vertical, la velocidad angular es
máxima y viceversa). |
|
 |
|
|
|
|
A partir de
los resultados de este análisis, se pueden
escribir las ecuaciones de las tres magnitudes
angulares que describen el movimiento de
oscilación del péndulo, tal comos se muestra en
la tabla adjunta. |
|

|
|
| |
|
Estos
valores permiten calcular la frecuencia angular del
movimiento, supuesto que sea armónico simple (w = 3,176 rad/s) y aplicando la expresión del péndulo simple,
conocida la longitud (L) del péndulo, también se puede
calcular la intensidad del campo gravitatorio. En este
caso se obtiene: g = L·w2 = 0,965·3,1762 =9,73 N/kg |
| |
|
Clic
aquí
descarga el archivo del análisis realizado con
Tracker. |
|
|
|
|
|