|
|
|
|
|
 |
|
EXPERIMENTOS Y TEORÍA SOBRE REFRACCIÓN DE LA LUZ |
|
|
|
| Experimentos
realizados por alumnos de Secundaria y de Bachillerato en el IES "Leonardo
da Vinci" de Alicante. |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
LEY DE LA REFRACCIÓN |
| |
| |
|
 |
|
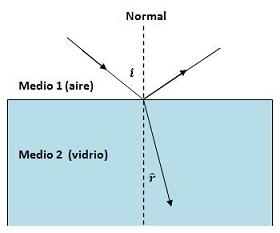
En el dibujo
adjunto, se muestra el recorrido de un rayo de luz
monocromática que incide sobre una
superficie plana que separa dos medios (en este
ejemplo, aire y agua). A partir del rayo
incidente, emergen de la superficie de
separación dos rayos: reflejado y refractado. El rayo reflejado se atiene a la ley de la reflexión
(el ángulo de incidencia es igual al ángulo de
reflexión) y
el rayo refractado se desvía con respecto al rayo
incidente siguiendo la ley de la refracción o
ley de Snell.
Dicha ley implica que cuando la luz
pasa
de un medio en el que tiene mayor velocidad
(en este ejemplo, el aire) a otro
medio en el que tiene menor velocidad (en este
ejemplo el vidrio), el rayo refractado se
acerca a la dirección normal (ángulo de
incidencia menor que el ángulo de refracción),
tal como muestra el dibujo.
En el caso contrario el rayo refractado se alejaría de la dirección normal (ángulo de incidencia mayor que el ángulo de
refracción). En 2º de
Bachillerato, la ley de Snell se deduce en clase
aplicando el principio de Huygens. |
|
|
|
|
Cuantitativamente,
la ley de Snell se expresa así: n1 ·
sen i = n2 ·sen r,
siendo n1 y
n2
los índices de refracción de la luz en el medio
incidente (1) y en el medio refractado (2) [El
índice de refracción de la luz en un medio es el
cociente entre su velocidad de propagación en el
vacío y su velocidad de propagación en el medio,
de forma que el índice de refracción de la luz en
el vacío es igual a la unidad y en cualquier
otro medio es mayor que la unidad]. |
|
|
|
|
|
|
| |
|
 |
| |
|
|
LÁMINA
PLANO-PARALELA |
| |
|
|
| |
|
 |
|
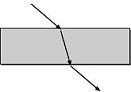
El estudio de la doble refracción de
un rayo de luz a través de una lámina plano-paralela (puede ser
de vidrio,
plástico,..) tiene un interés particular porque es uno de
los experimentos que apoya el modelo
ondulatorio de la luz. Si la luz fuera un chorro de
partículas sería muy difícil justificar que el rayo
recupere la dirección del rayo incidente después de
haberse desviado en el vidrio. En cambio, la teoría
ondulatoria prevé que eso es exactamente lo que debe
ocurrir. |
|
|
| |
|
|
| |
|
 |
|
 |
|
La fotografías adjuntas,
tomadas en el laboratorio por alumnos de 3º ESO y de 2º
Bachillerato, constatan
que al pasar del aire al vidrio el rayo de luz (luz
procedente de una bombilla de filamento en la fotografía de la izquierda, luz láser en la
de la derecha) se
desvía acercándose a la normal, y que a continuación, al
pasar del vidrio al aire, se vuelve a desviar alejándose
de la normal, con lo que recupera la dirección que
tenía en el aire el rayo incidente. |
|
|
| |
|
|
| |
Una cuestión importante que
conviene observar es el hecho de que después de cada
proceso de refracción, los rayos salientes tienen
menor intensidad que el rayo incidente. Así debe ser, puesto que
de acuerdo con el principio de conservación de la energía la
intensidad de la luz incidente se reparte en cada tránsito en
luz reflejada y luz refractada. |
|
| |
|
|
| |
|
 |
|
Los estudiantes
pueden constatar y/o aplicar la
ley de la refracción trabajando sobre fotografías
como las anteriores.
En este experimento,
tras medir los ángulos de
incidencia y de refracción, también calculan el índice
de refracción del vidrio. Además de hacerlo usando una
regla y un medidor de ángulos encima del papel, también
pueden trasladar la imagen a una animación Modellus
y usar (tal como muestra la imagen adjunta) una herramienta de medición
específica de ángulos de la que dispone este
programa. |
|
|
| |
|
|
|
| |
|
 |
| |
|
|
LENTES |
| |
|
|
| |
|
 |
|
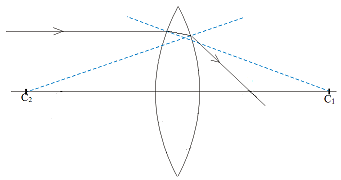
Para
trazar el camino de cualquier rayo de luz que atraviesa
una lente se tiene que aplicar la ley de la refracción
en dos tránsitos consecutivos de la luz: el primero del aire al
vidrio y el segundo del vidrio al aire. En cada uno de
estos procesos de refracción el ángulo de incidencia y
el ángulo de refracción se miden con respecto a una
dirección normal que pasa por el punto de la superficie
de separación entre los dos medios considerado y por el
centro de curvatura de dicha superficie de separación.
Estos conceptos se aplican en el dibujo
adjunto, que muestra el recorrido de un rayo
eje que atraviesa una lente biconvexa (centros de
curvatura C1 y C2, direcciones normales en líneas
punteadas de color azul). |
|
|
| |
|
|
| |
|
Las
fotografías mostradas a la derecha corroboran el dibujo anterior y
constatan que los rayos refractados por una lente
biconvexa avanzan por el otro lado en una dirección oblicua
orientada hacia el eje de la lente. Por tanto, dicha
lente es convergente, es decir, concentra la luz que procede
"del infinito"
(frentes de onda planos, rayos paralelos al eje) en un punto (foco de la lente).
|
|
 |
|
 |
|
|
| |
|
|
| |
|
 |
|
 |
|
Para
mostrar el foco lentes convergentes
se puede usar una puerta de triple rendija.
Algunas lentes convergentes son la lente plano-convexa
(fotografía de la izquierda), la lente biconvexa
(fotografía de la derecha), el menisco cóncavo-convexo
convergente (para que lo sea el radio de curvatura de la
primera cara, cóncava, tiene que ser menor que el de la
segunda, convexa), etc. |
|
|
| |
|
|
| |
|
 |
|
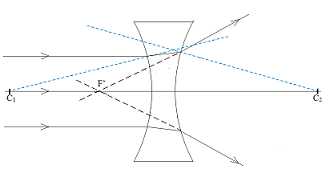
Los
estudiantes también experimentan la refracción a través
de lentes divergentes, como, por ejemplo, la lente
bicóncava. Tal como explica el diagrama de rayos adjunto
(a la izquierda), en la primera refracción a través de
esta lente (aire-vidrio), la luz se desvía acercándose a
la dirección normal y, por tanto, se aleja del eje de la
lente.
En la segunda (vidrio-aire) la luz se aleja de la
normal y también del eje. |
|
|
| |
|
|
| |
|
Las
fotografías adjuntas muestran la
divergencia de los rayos de luz, después de ser refractados por este
tipo de
lente. |
|
 |
|
 |
|
 |
|
|
| |
|
|
|
| |
|
 |
| |
|
|
IMÁGENES A TRAVÉS DE LENTES |
| |
|
|
| |
|
 |
|
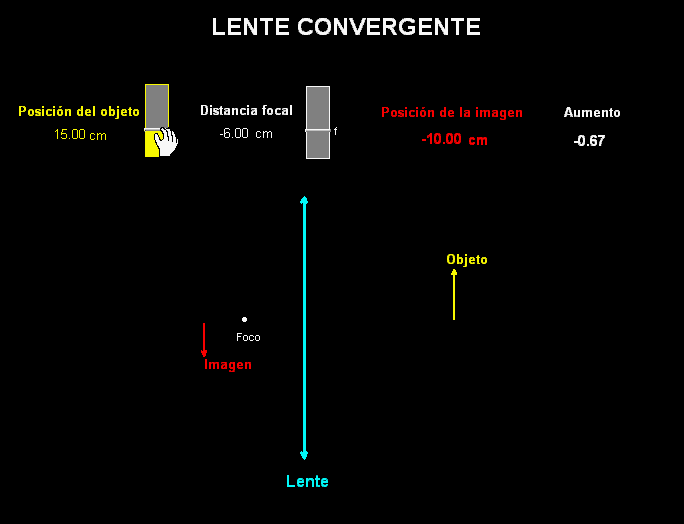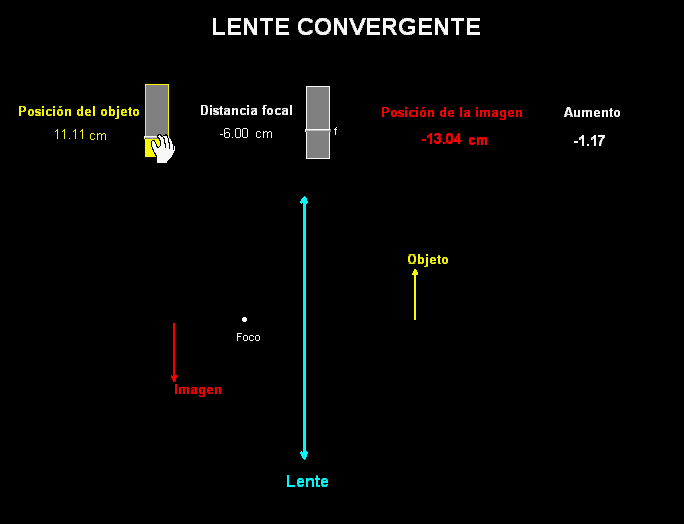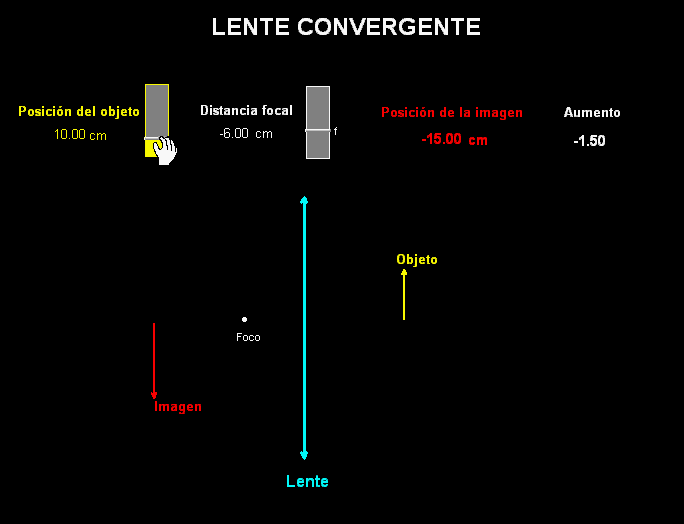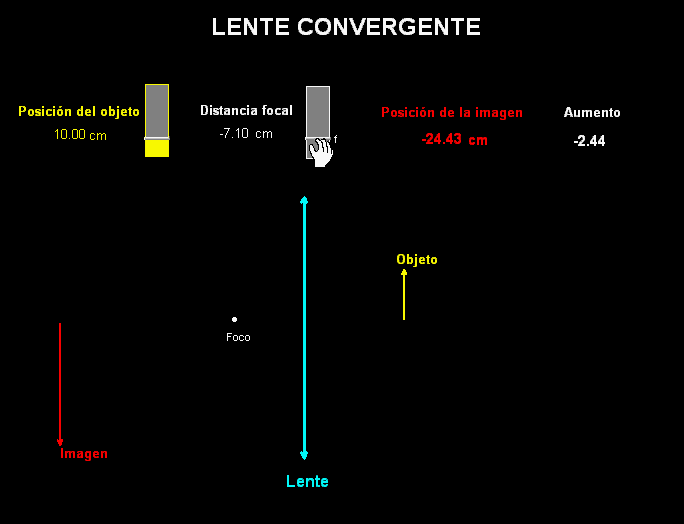
Los
experimentos sobre las lentes se han de completar
realizando en clase actividades teórico-prácticas (de
lápiz y papel) sobre el proceso de construcción de
imágenes a través de ellas.
Estas actividades se pueden
reforzar con ayuda de animaciones, como la adjunta, que,
como vemos construye y localiza la imagen de un objeto
extenso a través de una lente convergente (se
puede modificar a voluntad la posición de dicho objeto y
también la del foco de la lente).
La animación también
calcula el tamaño de la imagen con
respecto al del objeto.
Clic
aquí
para descargar la animación. Para abrirla en tu
ordenador
has de instalar
Modellus |
|
|
| |
|
|
| |
|
 |
|
Del mismo modo, esta segunda animación construye
y localiza la imagen de un objeto
extenso, ahora a través de una lente divergente.
Como la animación anterior, ésta también calcula el aumento
de la imagen con
respecto al objeto y se dispone de dos
controladores manuales, para modificar la
posición del
objeto y la distancia focal de la lente.
Si en
el caso de la lente convergente la imagen podía
ser real o virtual y, también, derecha o
invertida (dependiendo de la posición relativa
que con respecto al espejo tengan el objeto y la
lente) en el caso de usar una lente divergente,
la imagen siempre es virtual (se ve mirando a
través de la lente desde el lado opuesto a donde
se coloca el objeto) y de menor tamaño que el
objeto.
Clic
aquí
para descargar la animación. Para abrirla en tu
ordenador
has de instalar
Modellus |
|
|
| |
|
|
|
| |
|
 |
| |
|
|
REFLEXIÓN TOTAL |
| |
|
|
| |
|
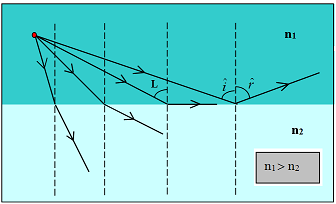
Cuando la luz viaja desde un medio donde tiene menor velocidad (índice de
refracción mayor) hasta otro donde tiene mayor
velocidad (índice de refracción menor), la refracción no
siempre es posible. Hay un ángulo máximo de incidencia a partir del cual la
luz sólo puede ser reflejada.
El dibujo adjunto ilustra
este concepto. En el medio 1 (puede ser, agua, vidrio,
etc.) una fuente luminosa emite luz en todas las
direcciones. Al refractarse esta luz hacia el medio 2
(puede ser, por ejemplo, aire), los rayos se desvían alejándose de la dirección normal
y a medida que el ángulo de incidencia aumenta
el ángulo de refracción también lo hace, pero no podrá superar el valor de 90º.
Así, el ángulo de incidencia correspondiente a un
ángulo de refracción igual a 90º es un ángulo límite y
todos los rayos incidentes con una inclinación mayor no
se pueden refractar. |
|
 |
|
|
| |
|
|
| |
|
 |
|
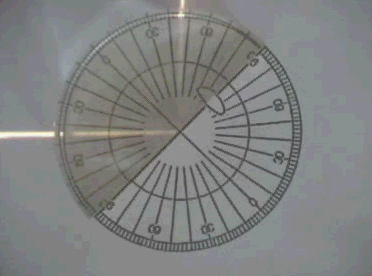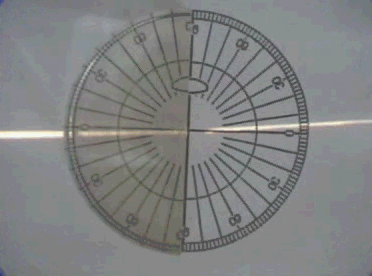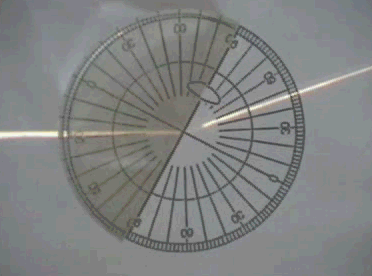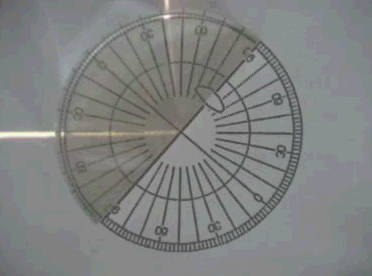
El clip de video adjunto,
gentileza del profesor jubilado Julio Santos Benito de
la Universidad de Alicante, muestra un experimento
sencillo para determinar el ángulo límite.
Un rayo láser
incide sobre la superficie de separación de los medios,
determinada, en este caso, por un transportados de
ángulos graduado.
Al ir rotando el transportador va
aumentando el ángulo de incidencia del rayo láser y
también, lógicamente, el correspondiente ángulo de
refracción. Cuando este segundo ángulo (refracción)
alcanza el valor de 90º, la luz láser ya no pasa al otro
medio y podemos determinar directamente con el
transportador el ángulo límite. A partir de ahí,
mientras el transportador sigue rotando, comprobamos que
el rayo láser es reflejado totalmente y que se cumple en
todo momento la ley de la refracción (es decir, el
ángulo incidente es igual al ángulo reflejado) |
|
|
| |
|
|
| |
|
Las
fotografías adjuntas las tomaron en el laboratorio
alumnos de 2º Bachillerato. Normalmente un rayo de luz láser no se vería,
ni en el agua, ni en el aire (fotografía más a la
izquierda). Ahora bien, disolviendo en el agua una
gotita de leche, ocurre que las partículas de la leche
disuelta actúan como focos secundarios que sí son
visibles y, en conjunto, muestran la trayectoria del
rayo.
Entonces, inclinando la fuente de luz láser se
puede comprobar que dicho rayo se refleja totalmente en
la superficie de separación con el agua (fotografía más
a la derecha). |
|
 |
|
 |
|
|
| |
|
|
| |
|
 |
|
 |
|
Para observar la reflexión total en el
laboratorio, los estudiantes también pueden usar una
pieza de plástico con forma prismática.
En la
posición que muestran las
fotografías el rayo de luz (luz blanca
en la fotografía más a la izquierda y luz láser en
la situada más a la derecha) penetra en el vidrio desde
el aire por una cara menor del prisma y luego incide sobre la cara mayor
con un ángulo superior al ángulo límite. Por
tanto, ahí no se refracta hacia el aire,
sino que se refleja totalmente. Este rayo,
totalmente reflejado dentro del plástico, incide
después sobre otra cara menor del prisma con un ángulo
mucho menor, con el que puede salir de nuevo al
aire. |
|
|
|
|
| |
|
|
|
| |
|
 |
| |
|
|
ALGUNAS APLICACIONES |
| |
|
|
| |
 |
|
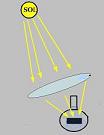
La
propiedad que tienen las lentes convergentes de
dirigir la luz hacia el foco tiene variadas
aplicaciones.
Una de ellas es concentrar luz solar en un
área pequeña con intención de acumular energía térmica.
El esquema adjunto representa lo que podría ser un
concentrador solar casero aplicando esta idea. Los
rayos del Sol inciden sobre la lente y son refractados
por ella hacia el foco, donde podríamos colocar un cuerpo negro
sumergido en agua. Como el cuerpo recibe de manera
concentrada energía de la luz colectada en un
área mucho mayor, su temperatura se eleva notablemente
y calienta el agua que lo rodea. |
|
|
| |
|
|
| |
|
Este método no se usa en la práctica para el
calentamiento de agua en gran escala, pero ayuda
a entender otras aplicaciones que sí tienen un desarrollo industrial
importante, como, por ejemplo, algunos tipos de paneles
concentradores de
energía solar fotovoltaica.
El que muestra
la fotografía contiene una
serie de lupas
que concentran luz en un pequeño
espacio, donde otro material (de coste mucho más
elevado) recoge la energía. |
|
 |
|
|
|
|
| |
|
|
| |
|
 |
|
Como anécdota curiosa se puede mencionar una
noticia de 2010 sobre un incendio que se produjo en una
vivienda de la localidad estadounidense de Dubois
(Wyoming).
Un empleado del correo escuchó una alarma de
incendios dentro y pidió ayuda a la policía. La policía
determinó que el incendio se había producido porque la
luz solar que entraba por la ventana era
concentrada por una lupa que apuntaba a una pila de
correspondencia. El incendio se pudo controlar antes de
que los daños a la casa fueran totales (el dueño de la
vivienda no estaba en la casa cuando se produjo el
fuego). |
|
|
| |
|
|
| |
|
Terminamos comentando una aplicación de la
reflexión total de enorme utilidad: La fibra óptica.
Básicamente es un hilo muy fino de material plástico por
el que se envía luz. El haz de luz no sale del plástico porque cada vez que incide
en la superficie de separación con el exterior, lo hace
con un ángulo de reflexión mayor que el ángulo límite de
reflexión total. |
|
 |
|
|
| |
|
|
| |
 |
|
 |
|
 |
|
La fotografía de la izquierda muestra un haz de
cables de fibra óptica fibras óptica. Las otras dos
fotografías corresponden a dos experimentos realizados
en el laboratorio y constatan que la luz, al igual que
hace en la fibra óptica, viaja a lo largo de una varilla
recta de plástico y a lo largo de un capilar de vidrio
doblado. |
|
|
| |
|
|
| |
Las fibras ópticas se utilizan ampliamente en
telecomunicaciones y permiten enviar gran cantidad de
datos a una gran distancia, con velocidades similares a
las de radio y superiores a las de un cable
convencional. Son el medio de transmisión por excelencia
al ser inmunes a las interferencias electromagnéticas y
también se utilizan para redes locales. Para minimizar
la disminución paulatina de la intensidad de la luz
transportada debida a la absorción, el material
utilizado en la fibra óptica tiene índice de
transparencia muy elevado (10 km de fibra atenúan la luz
lo mismo que 2 mm de vidrio de ventana). Como dato
ilustrativo, podemos decir que si el mar fuera tan
transparente como algunas fibras ópticas veríamos el
fondo de los océanos con total claridad. |
|
| |
|
|
|
| |
|
 |




