|
|
|
 |
|
SEGUNDA LEY
DE GAY-LUSSAC |
|
|
| Experimentos
realizados por alumnos de Bachillerato en el IES Leonardo Da Vinci de
Alicante. |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
HIPÓTESIS |
| |
| |
|
Al estudiar el comportamiento
físico de los gases, se plantea, a modo
de hipótesis, que la presión de un gas encerrado
en un recipiente ha de depender del volumen, la
temperatura y la cantidad de gas (expresable
como número de moléculas, masa, densidad, número
de moles,..).
Acerca de la relación entre la temperatura y la
presión
(suponiendo fijo el volumen y la cantidad de gas),
se espera que al ir aumentando la
temperatura de un gas encerrado en un recipiente
hermético, aumente la presión absoluta que
ejerce sobre las paredes del recipiente.
|
| |
|
 |
|
La hipótesis se fundamenta en el modelo
cinético-corpuscular de la materia, según el cual los gases
estarán formados por muchas partículas muy pequeñas,
separadas entre sí por grandes distancias en comparación con
su pequeñísimo tamaño, y moviéndose en todas las direcciones
(gas ideal). Según este modelo, la presión ejercida por el gas
se debe a los choques de sus partículas con las paredes del recipiente
y la temperatura es una medida macroscópica de la energía cinética media de
las moléculas.
Por tanto, al aumentar dicha energía cinética debería aumentar
la frecuencia de los choques y su intensidad. De forma más precisa, se espera que la
temperatura y la presión sean directamente proporcionales (Segunda
ley
de Gay-Lussac). |
|
|
|
El propósito del experimento es contrastar
esta hipótesis y otras previsiones del modelo
relacionadas con ella. |
|
|
|
| |
|
| |
|
 |
| |
|
DISEÑOS EXPERIMENTALES |
| |
| |
|
 |
|
Un diseño experimental, que utiliza el
profesor Mikel Etxaniz con alumnos de 1º
Bachillerato, se basa en calentar el
aire de un matraz “al baño María”
después de introducirlo en un vaso de
precipitados con agua. Un sensor de
presión se conecta al matraz y otro de
temperatura se introduce en el agua.
Con
este montaje se puede hacer variar la
temperatura del agua desde la
temperatura ambiente (unos 20º C) hasta
una temperatura elevada, próxima a la de
ebullición (algo más de 90º C). La fotografía adjunta corresponde al experimento pionero que
se realizó en los
cursos 2002-03 y 2003-04, formando parte del trabajo sobre "Los Gases"
(Premio Nacional "Giner de los Rios"
en 2004). |
|
|
|
|
Otro diseño experimental, utilizado
en 2009 por
estudiantes de 1º Bachillerato en el laboratorio del Instituto
"Leonardo da Vinci",
usa un calentador magnético, un matraz y
el sensor doble de presión-temperatura. |
|
|
|
 |
|
En el matraz se introduce agua y se cierra
con un tapón aforado que permite insertar un tubito de plástico
(que a su vez conecta al sensor de presión) y
el extremo del detector de temperatura del propio sensor.
Después de encajar estos elementos
queda encerrada
una cierta cantidad de aire entre el tope del agua que
incluye el matraz y el final del tubo de plástico donde se sitúa
el detector de presión. Con el calentador
magnético conectado, el agua encerrada en el sensor se va calentando
paulatinamente, y con ella lo hace el aire encerrado.
En la
medida en que no se produzca evaporación de dicho agua, la
cantidad y el volumen del aire permanecen razonablemente constantes y se pueden obtener mediciones de
la evolución de la presión y la
temperatura, así como la relación entre ellas.
|
|
|
| |
|
|
|
|
| |
|
 |
| |
|
RESULTADOS |
| |
|
|
|
 |
|
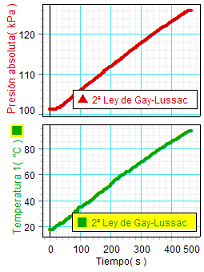
Se muestran
muestran gráficas obtenidas directamente
en el experimento, que representan por
separado la
evolución de la presión y la evolución
de la temperatura. Como es lógico ambas
magnitudes
aumentan durante el tiempo en el que se
está calentando el agua del matraz (que,
a su vez, calienta el aire encerrado) |
| |
| |
 |
|
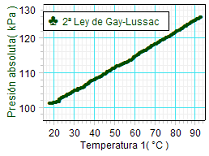
Para obtener
la relación directa entre la
temperatura y la presión, se combinan
las dos graficas. Como se observa, los
resultados obtenidos parecen confirmar a
primera vista la hipótesis (en el sentido de
presentar una una
relación lineal entre ambas magnitudes),
pero se ha de fijar la atención en que no muestran una relación
proporcional entre la presión y el
volumen.
La relación no es del tipo P = K·T,
puesto que la gráfica no pasa,
ni mucho menos, por el origen. |
|
|
|
|
Resulta muy instructivo debatir este
extremo con los estudiantes,
conduciéndoles a la búsqueda del mínimo
valor de la temperatura (es decir, de la
temperatura que teóricamente tendría el
gas si llegara a no ejercer presión), el
"mítico" cero absoluto. |
|
| |
|
|
|
|
| |
|
 |
| |
|
TEMPERATURA MÍNIMA (BÚSQUEDA DEL CERO
ABSOLUTO) |
| |
| |
|
 |
|
 |
|
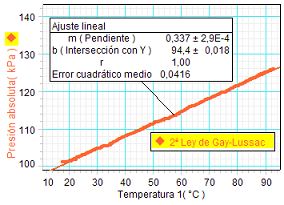
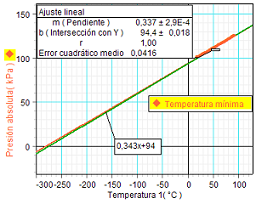
A la izquierda se muestra el
resultado del ajuste lineal llevado a cabo sobre
los resultados experimentales (línea de color naranja en ambas
gráficas). Se observa que se ajustan muy bien a
una recta y que ésta corta al eje de presiones en un
valor positivo (94.4 kPa).
En la gráfica a
la derecha se ha modificado la escala de
representación para buscar el punto de corte con
el eje de temperaturas, que, como se observa,
está en la zona próxima a los teóricos
- 273.16 ºC. |
|
| |
|
 |
|
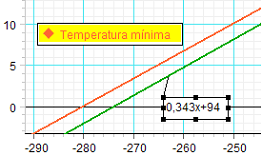
Ampliando la escala se
observa dicha temperatura con mayor detalle, la
cual que, atendiendo al ajuste realizado por el
programa, sería de -280 ºC.
Adicionalmente, se ha añadido otro ajuste lineal
definido por el usuario (línea de color verde).
Como se observa, con una ligerísima modificación
del valor de la presión para t = 0ºC (de
94,4 kPa a 94 kPa) el ajuste nos lleva
a la temperatura mínima teórica (- 273 ºC).
Se trata, evidentemente de una trampa
realizada deliberadamente sobre los resultados,
pero que permite, por otro lado, explicar que
ajustar es ir acercando paulatinamente la
función teórica a la real. |
|
| |
|
|
|
| |
|
 |
|
|
|
EXPRESIÓN DE LA SEGUNDA LEY DE GAY-LUSSAC |
| |
| |
|
Para expresar la segunda ley de Gay-Lussac
es preciso desplazar previamente la escala de
temperaturas a grados Kelvin, lo que se puede hacer
modificando cada valor medido (incrementando las
temperaturas en 273,15 unidades) o,
también modificar la relación matemática que se deriva
del ajuste realizado. |
| |
|
Con la temperatura expresada
en unidades Kelvin, la relación entre la presión
y la temperatura debería ser: P = K·T. Como
T = t + 273,15, tenemos que:
P = K (t + 273.15) = K·t + Po (la constante K
es igual en las dos escalas de temperatura)
El ajuste realizado sobre los
valores experimentales proporciona la siguiente
relación:
P = 94,2 + 0,337·t
(estando la presión en kPa y la
temperatura en ºC)
Por tanto, podemos expresar
la segunda ley de Gay-Lussac para este caso así:
P / T = 0,337 K/kPa (para una cantidad
constante de aire y a un determinado volumen del
mismo encerrado en el matraz) |
|
| |
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Puedes descargar el
resultado original del experimento que
se describe en esta página. Para abrir el archivo se necesita el programa DataStudio, del que tienen
licencia bastantes departamentos de Física y Química de
institutos de Enseñanza Secundaria. |
|

