|
 |
|
PULSO AMORTIGUADO
EN UN MUELLE |
|
|
|
Experimento realizado por estudiantes de Bachillerato en el IES "Leonardo da Vinci" de Alicante |
|
|
| |
|
PLANTEAMIENTO
Y PROPÓSITO DEL EXPERIMENTO |
| |
|
La presencia insoslayable
de rozamientos (con el aire, con superficies de
contacto, etc.) provoca que las oscilaciones de los
sistemas físicos reales (por ejemplo: un muelle, un
péndulo, una bola que rueda dentro de un cuenco, etc.)
sean amortiguadas.
Teniéndolo en cuenta, nos proponemos
realizar un estudio teórico y
experimental de este tipo de oscilaciones, el cual se
inicia pidiendo a los alumnos que dibujen,
a modo de hipótesis, una gráfica cualitativa de la
evolución de la posición de un muelle real, que realiza
oscilaciones amortiguadas. |
|
 |
|
|
|
 |
|
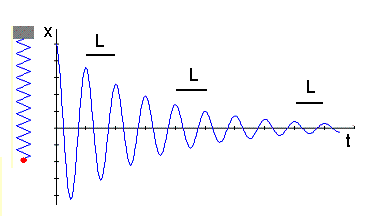
Interesa ver despacio esta gráfica para que se entienda
que la amortiguación afecta a la amplitud, pero no al
periodo, tal como
se quiere enfatizar en el dibujo adjunto.
Hecha esta
aclaración,
se puede afrontar el problema de reflejar la amortiguación
en las ecuaciones del movimiento. A este respecto, los alumnos plantean una fuerza de rozamiento opuesta a la
fuerza de recuperación del muelle. Si previamente han estudiado
la caída libre con rozamiento, saben que las fuerzas de rozamiento en el seno de un
fluido dependen de la velocidad de penetración en el
mismo. Y ello les lleva a concebir la hipótesis de una fuerza de
rozamiento del tipo:
Froz = - b·v
(siendo v la velocidad y b un coeficiente de
amortiguación) |
|
| |
|
El objetivo de este experimento en contrastar esta hipótesis con
ayuda de Modellus. Para ellos se analizará la
correspondencia entre el movimiento de un pulso amortiguado
producido en un muelle y el
movimiento de una partícula virtual sobre la que se ejerce,
además de la fuerza de recuperación del muelle, una fuerza de rozamiento de
este tipo. |
|
| |
|
DISEÑO EXPERIMENTAL |
| |
|
Para realizar el estudio
planteado se requiere un video que recoja el movimiento
del pulso amortiguado, como los dos que, a modo de
ejemplo, se muestran seguidamente. |
| |
|
|
| |
|
Además de esta medición, se
determinó el periodo de las oscilaciones usando un
cronómetro digital. |
|
| |
|
ANÁLISIS
EXPERIMENTAL CON MODELLUS
|
| |
|
Una vez insertado el video
en una página
de Modellus, se usa la herramienta de medida que proporciona el
programa para obtener la equivalencia entre pixels
y metros (el dato de referencia es la amplitud máxima
de las oscilaciones) y, en la ventana
reservada al modelo físico-matemático, se escribe la ley
diferencial del movimiento,
considerando la acción de la fuerza de
recuperación del muelle (F = - k·x) y la
fuerza de amortiguación (Froz
= - b·v). |
| |
|
 |
|
Se puede añadir la
figura de un muelle (configurándola para que oscile
ateniéndose al modelo) y se gráficas de algunas
magnitudes (elongación, velocidad, etc.).
Finalmente,
se coloca un cursor
para
variar a voluntad el valor de coeficiente de
amortiguación y se prueban valores de
dicho coeficiente,
buscando la concordancia entre el movimiento de
un papelito de color rojo enganchado al muelle y
el movimiento de una partícula virtual del mismo
color.
Clic
aquí
descarga la animación para
Modellus 2.5 (32 bits)
Clic
aquí
la descarga para
Modellus 3 (64 bits) |
|
|
| |
|
En el experimento realizado en
el laboratorio, los estudiantes trabajaron en equipos de
4: dos alumnos sujetaban los extremos del muelle, otro
producía el pulso y el cuarto filmaba el movimiento. El
profesor les entregó una animación Modellus
incompleta, donde ellos debían insertar su video, y
escribir su modelo físico-matemático (teniendo en cuenta
el valor de la relación entre píxeles y metros,
que correspondiera a cada equipo).
Clic
aquí
descarga la animación (Sólo para
Modellus 2.5 (32 bits). |
|
 |
|
|