| |
|
|
| |
|
PLANTEAMIENTO Y PROPÓSITO DEL EXPERIMENTO |
| |
|
Una consecuencia notable de la hipótesis de
Galileo sobre el movimiento de proyectiles,
aplicada al tiro horizontal, es el hecho de que
el tiempo empleado por una pequeña pelota en
llegar al suelo cuando se lanza horizontalmente
con cualquier velocidad coincide con el empleado
por ella misma, cuando, en lugar de ello, se
deja caer verticalmente desde el mismo punto.
En otro trabajo práctico hemos visto cómo se
puede contrastar esta derivación de la hipótesis
a través del estudio de un clip de video que
recoge ambos movimientos, generados
simultáneamente.
Nos proponemos ahora utilizar
el programa Tracker, para añadir a aquél
estudio algunos análisis cuantitativos sobre los
movimientos, ya filmados, de ambas pelotas.
|
|
 |
|
|
|
|
|
RESULTADOS DE LOS
ANÁLISIS |
|
|
|
a
partir del análisis de las posiciones determinadas en la
imagen del video (por tanto, partiendo de los datos
experimentales), se pueden obtener con Tracker
diferentes gráficas sobre la evolución de las magnitudes
cinemáticas del movimiento filmado. El programa obtiene
la función matemática que mejor describe el movimiento
de cada una de las dos pelotas por ajuste de mínimos
cuadrados y permite así obtener cuantificar las
magnitudes estudiadas. Mostramos, a modo de ejemplo, las
siguientes (Clic
aquí
descarga el archivo de los análisis): |
|
|
|
 |
|
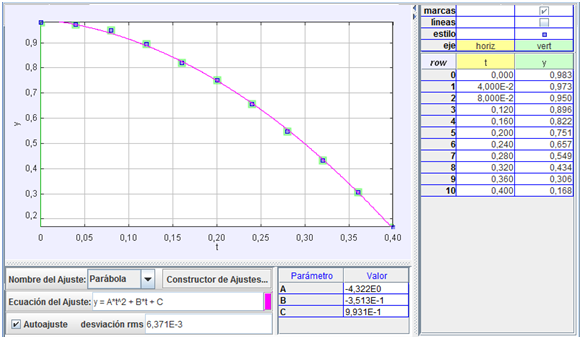
Gráfica
de la posición de la pelota en caída libre
como vemos, la
ecuación del mejor ajuste es, como exige la
hipótesis, la de un movimiento casi vertical y
uniformemente acelerado. Los parámetros B y
C,
obtenidos en el ajuste, tienen valores muy
pequeños, lo que es coherente con el hecho de
que el movimiento de caída de esta pelota (la
situada más a la izquierda en la imagen
fotográfica anterior) sigue una trayectoria
cercana a la dirección vertical.
En cuanto al
parámetro A, su valor representa a la mitad de
la aceleración, lo que nos daría un valor de
ésta del orden de 8,7 m/s2. Si la
trayectoria de esta pelota fuese totalmente
vertical y la fricción con el aire se pudiera
considerar totalmente despreciable, el valor
teórico de la aceleración debería ser muy
próximo a g (9,8 m/s2).
|
|
| |
|
 |
|
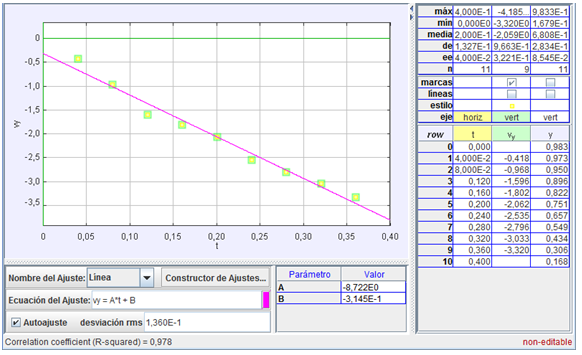
Gráfica
de la componente vertical de la velocidad de la
pelota en caída libre
El mejor ajuste
corresponde, como se esperaba, a una relación
lineal entre la velocidad vertical y el tiempo,
tal como exige la ley que representa la
evolución de la velocidad en un movimiento
uniformemente acelerado.
La aceleración en este
caso está representada por el coeficiente B, de
modo que, coherentemente con el análisis de la
gráfica de la posición vertical, tendrá un valor
de 8,7 m/s2.
|
|
|
|
|
 |
|
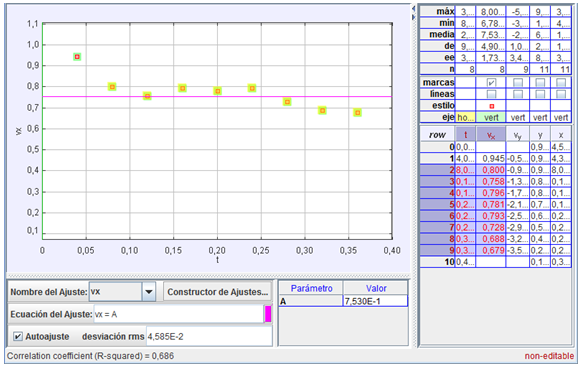
Gráfica
de la componente horizontal de la velocidad que
describe el tiro horizontal
Este último
análisis se refiere a la componente horizontal
de la velocidad de la pelota que sigue una
trayectoria oblicua (situada más a la derecha en
la imagen fotográfica anterior)
Vemos que el
mejor ajuste para esta magnitud se obtiene
suponiendo que esta velocidad horizontal es
constante, como exige la hipótesis de Galileo.
En este caso, el valor de esta velocidad
constante es obviamente el del único parámetro,
A, por tanto, tenemos vx = v0x
= 0,75 m/s.
|
|
|
|
|
|