|
 |
|
MOVIMIENTO CIRCULAR
DE UNA PELOTITA, DE UN DISCO Y DE UN TREN DE JUGUETE |
|
|
|
Experimentos
realizados por alumnos de Secundaria y de Bachillerato del IES Leonardo Da Vinci de Alicante |
|
|
| |
|
PROPÓSITO DEL
EXPERIMENTO |
| |
|
Se quiere realizar un estudio experimental sobre la
cinemática del
movimiento circular uniforme (MCU).
Para ello, se filmará un clip de video
de un movimiento de este tipo y se usará el programa
Modellus para cotejar la concordancia entre el
movimiento filmado (real) y un movimiento virtual acorde
con las leyes teóricas del MCU. |
|
 |
|
|
| |
|
VIDEOS DE
MOVIMIENTOS CIRCULARES |
| |
|
|
|
|
|
Después de filmar
estos movimientos se usa un programa gratuito de
tratamiento de videos para recortar el pedazo escogido
para el análisis y comprimir el clip de video
correspondiente. |
|
| |
|
ANÁLISIS
EXPERIMENTAL
CON
MODELLUS |
| |
|
El análisis experimental
se inicia volcando el video sobre una página
de Modellus y usando la herramienta de medición del
programa para determinar la equivalencia entre cm y
píxeles (usando como referencia el radio de la
circunferencia).
|
| |
|
 |
|
Con
este dato y
el del periodo del movimiento (medido doblemente: al
hacer el experimento y sobre la propia grabación) los
estudiantes escriben el modelo físico-matemático de la
simulación, conformado por la ecuación de las
componentes (x , y) de un
movimiento circular uniforme.
El
movimiento de la pelotita no es realmente
uniforme, porque interviene el rozamiento con el
plato y con el aire. Sin embargo, dicho
rozamiento no es excesivo, por lo que nos
planteamos que se pueda despreciar al considerar
una sola vuelta.
Al hacer correr la
animación, se comprueba
la bondad de esta previsión, pues, para una vuelta, se obtiene una buena concordancia
entre el movimiento que se deduce de las leyes escritas
en el modelo (simulación) y el de la pelotita
real (filmada).
Clic
aquí
descarga la animación para
Modellus 2.5 (32 bits)
Clic
aquí
la descarga para
Modellus 3 (64 bits) |
|
|
| |
|
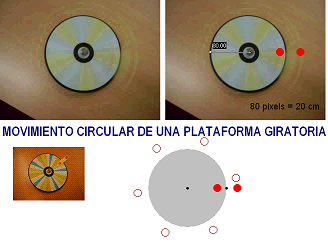
En el otro
experimento el periodo se mide únicamente sobre la
filmación, puesto que el disco gira demasiado
rápido, como para poder determinarlo con un cronómetro.
Además se requiere ralentizar la filmación a una escala de
1/200 y, aún así, cuesta seguir con la vista las zonas coloreadas de la plataforma.
No obstante, este dispositivo permite
estudiar algunas cuestiones interesantes ausentes del
experimento anterior. Por ejemplo, se analiza el
movimiento de dos puntos de la plataforma situados a
diferentes distancias del centro de la circunferencia.
Y, se puede extender el análisis a varias vueltas, sin pérdida
sensible de la velocidad por del disco.
Clic
aquí
descarga la animación para
Modellus 2.5 (32 bits)
Clic
aquí
la descarga para
Modellus 3 (64 bits) |
|
|
 |
|
| |
|
Todo ello, tras
obtener una buena concordancia entre el movimiento que se
deduce de las leyes escritas en el modelo (simulación) y
el de los puntos del disco (filmada) |
|