|
|
|
 |
|
CHOQUES DE
DOS CARRITOS EN SITUACIONES DIVERSAS |
|
|
| Experimentos
realizados por alumnos de Bachillerato en el IES Leonardo Da Vinci de
Alicante. |
|
|
| |
| |
 |
PROPÓSITO DE LOS
EXPERIMENTO. EJEMPLOS FILMADOS |
 |
RESULTADOS DE UNO DE
LOS EXPERIMENTOS |
 |
CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO |
 |
CÁLCULO DEL
COEFICIENTE DE RESTITUCIÓN |
 |
ARCHIVOS DE
DATASTUDIO |
|
|
|
|
|
|
|
|
|
|
PROPÓSITOS DE LOS EXPERIMENTOS.
EJEMPLOS FILMADOS |
| |
| |
|
Después de haber realizado
varios experimentos sobre choques de carritos
buscando algunas situaciones en "simplificadas"
(por ejemplo, choque de un carrito sobre otro
impulsando al segundo, choque de un
carrito sobre otro, siguiendo ambos unidos,
etc..) nos proponemos que los diversos grupos
estudien choques de dos carritos, en diferentes
situaciones, por ejemplo: teniendo los carritos
masas diferentes, rebotando ambos en sentidos
opuestos al que tenían antes del choque, etc.
Cada grupo elige alguna de estas
situaciones y todos han de comprobar en su
experimento el grado de verificación de la ley
de conservación de la cantidad de movimiento. A modo de
ejemplo se pueden observar los videos adjuntos
tres situaciones experimentales diferentes que
se pueden plantear. |
| |
|
|
| |
|
|
|
|
| |
|
 |
| |
|
RESULTADOS DE UNO
DE LOS EXPERIMENTOS |
| |
|
|
| |
|
 |
|
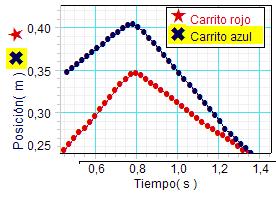
A la izquierda se adjunta la
gráfica obtenida por los estudiantes en el
experimento que corresponde a la tercera de las
filmaciones mostradas más arriba. Para
obtenerla, los estudiantes colocaron dos
sensores de posición en los extremos del carril,
de tal forma que uno de ellos registra el
movimiento del carrito rojo y otro el del
carrito azul.
De entrada, esta gráfica
muestra un perfil cualitativo muy satisfactorio.
Teniendo en cuenta que los dos carritos tienen
la misma masa, es lógico esperar que las
pendientes de las gráficas de la posición (que
representan las correspondientes velocidades de
los dos carritos antes y después del choque) se
compensen. Cualitativamente se observa que es así: el carrito rojo parece tener mayor velocidad
(mayor pendiente) que el azul antes del choque. La situación es la
opuesta después del choque.
|
|
|
|
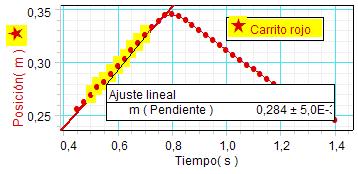
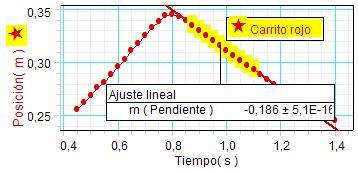
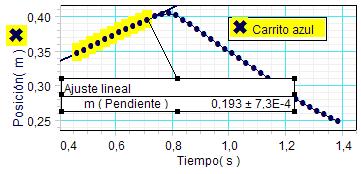
Para obtener los valores de tales velocidades
los estudiantes realizan ajustes lineales en
ambas gráficas, antes y después del choque, lo
que proporciona los resultados siguientes. |
|
|
| |
 |
|
 |
|
| |
Velocidad carro rojo antes del choque:
0,284 m/s |
|
Velocidad carro rojo después del choque:
0,186 m/s |
|
|
|
|
| |
 |
|
 |
|
| |
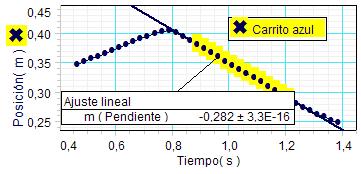
Velocidad carro azul antes del choque:
0,193 m/s |
|
Velocidad carro azul después del choque:
0,282 m/s |
|
|
|
|
|
|
|
|
| |
|
 |
| |
|
CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO |
| |
| |
|
Para que se cumpla la ley de
conservación de la cantidad de movimiento del
sistema formado por los dos carritos, se
requiere que: |
| |
|
psist-antes
= psist-después → mrojo · vrojo-antes
+ mazul · vazul-antes
= mrojo · vrojo-después
+ mazul · vazul-después |
| |
|
Hay que tener cuidado
al sustituir los valores experimentales en esta
expresión, particularmente al especificar el
signo de la velocidad de cada carrito antes y
después del choque. Los signos que proporciona
el programa no son correctos porque se han usado
dos sensores de movimiento que actúan como
origen de un sistema de referencia diferente
para cada carrito. Se requiere, por tanto,
olvidar los signos aportados por el programa y
adoptar un único sistema de referencia. En este
caso, adoptamos uno con origen en el sensor que
toma las medidas de la posición del carrito
rojo. Teniendo en cuenta que los dos carritos
tienen la misma masa, m, escribimos: |
| |
|
m ·
0,284 + m ·
(- 0,193) = m
·
(- 0,186) + m ·
(0,282)
→
0,091 · m =
0,096 · m
|
| |
|
Este resultado dice que la
cantidad de movimiento del sistema antes y
después del choque difiere en un 6%, lo que, teniendo en cuenta el margen de
imprecisión de los sensores, es compatible con
la ley de conservación la cantidad de
movimiento. |
| |
|
|
|
|
| |
|
 |
|
|
|
CÁLCULO DEL
COEFICIENTE DE RESTITUCIÓN |
| |
| |
|
Para calcular el
coeficiente de restitución (cociente
de la diferencia entre las velocidades de
acercamiento y las de alejamiento de los
carros), hay que tener cuidado una vez más
con los signos de las velocidades. Se obtiene: |
| |
|
Coeficiente de restitución = (0,284
- 0,193)/(0,282 - 0,186) = 0,948 |
| |
|
Lo que significa que después
del choque se restituyó a los carros un 94,8 % de
la energía cinética que portaban antes del
choque. Por tanto, el choque fue prácticamente
elástico. |
| |
|
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Puedes descargar el
resultado original de
los experimentos
descritos en esta página. Para abrir los archivos se necesita el programa DataStudio, del que tienen
licencia bastantes departamentos de Física y Química de
institutos de Enseñanza Secundaria. |
|