Choque de dos carritos con arrastre de uno de ellos

CHOQUE DE DOS CARRITOS CON ARRASTRE DEL SEGUNDO

Experimentos realizados por alumnos de Bachillerato en el IES Leonardo Da Vinci de Alicante.

		PROPÓSITO DEL EXPERIMENTO Y PREDICCIÓN
		DISEÑO EXPERIMENTAL Y CLIP DE VIDEO DEL MOVIMIENTO
		RESULTADOS
		ARCHIVOS DE DATASTUDIO

PROPÓSITO DEL EXPERIMENTO Y PREDICCIÓN

El objetivo del experimento es estudiar el choque de dos carritos en una situación sencilla en la que se puede prever el resultado experimental mediante la aplicación del principios de conservación de la cantidad de movimiento.

La situación elegida es un choque de un carrito (rojo en la fotografía) sobre otro, inicialmente en reposo (azul), de tal forma que, tras el choque los dos carritos ruedan juntos (como se observa en las fotografías, los carritos se enfrentan por una cara que tiene una superficie de fieltro que asegurará que continúan unidos. Los estudiantes tienen que resolver el problema antes de hacer el experimento, cuyo objetivo será comprobar si la velocidad del conjunto resuelvan el problema y predigan la velocidad del conjunto después del choque.

Para resolver el problema, los equipos expresan la cantidad de movimiento del sistema que forman los dos carritos antes y después de chocar.

p_antes = m_coche-rojo · v_coche-rojo		p_después = (m_coche-rojo + m_coche-azul) · v

Despreciando los rozamientos, tenemos que la suma de las fuerzas exteriores que se ejercen sobre el sistema (el peso de cada carrito y la normal) es cero. Por tanto, la cantidad de movimiento del sistema debe de permanecer constante. Como la masa de ambos carritos es la misma [ m_coche-rojo= m_coche-azul] , al exigir, p_antes = p_después, se obtiene que la velocidad del conjunto después del choque tiene que ser la mitad de la velocidad a la que se lanza el coche rojo [ v = (v_coche-rojo)/2].

DISEÑO EXPERIMENTAL. CLIP DE VIDEO DEL EXPERIMENTO

Para obtener resultados de las velocidades antes y después del choque los estudiantes colocan en el extremo del carril un sensor de movimiento y se proponen realizar una doble medición de la velocidad: a partir de la gráfica de la posición y de la propia velocidad.

Tal como se observa en el clip de video adjunto, un estudiante del equipo se ocupa de manejar el ordenador y otro de lanzar el carrito. Con objeto de obtener suficientes valores de la posición y, al mismo tiempo, asegurar una buena precisión en los mismos, los equipos configuran el sensor a una frecuencia de 40-50Hz (40-50 mediciones por segundo)

RESULTADOS

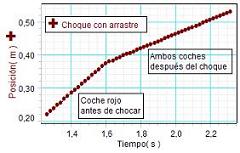
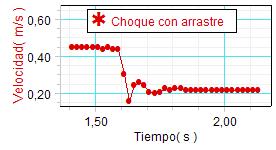
A la izquierda se muestra la gráfica de la evolución de la posición medida del carrito rojo tomada desde su espalda. Responde cualitativamente a lo esperado, puesto que revela dos movimientos casi uniformes antes y después del choque y un brusco descenso de la velocidad tras chocar. La gráfica correspondiente de la velocidad (a la derecha) confirma el resultado y además aporta unos valores de la velocidad antes y después del choque que corroboran la predicción (la velocidad después es próxima a la mitad de la inicial)

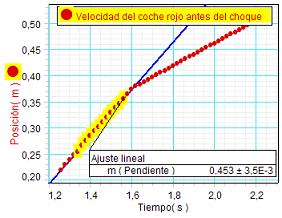
Para determinar las velocidades con mayor precisión, los estudiantes trabajan con la gráfica de la posición. Escogen unas pocas posiciones antes del choque (pero, lo más próximo posible a él, puesto que, aunque el rozamiento de los carritos en el carril es muy pequeño, no es nulo) y otras tantas después, y realizan sendos ajustes lineales. Las pendientes correspondientes representan a la velocidad antes y después del choque.

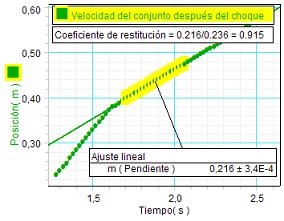
Como se observa, estos análisis también confirman la predicción de que después de chocar, los dos carritos juntos tienen casi la mitad de la velocidad que tenía antes del impacto el carrito de color rojo. La diferencia entre el valor experimental de la velocidad del conjunto después del choque, 0.216 m/s, y el valor teórico, 0.226 m/s (0.453/2) es inferior al 5%, por tanto, muy aceptable teniendo en cuenta el margen de imprecisión de los sensores.

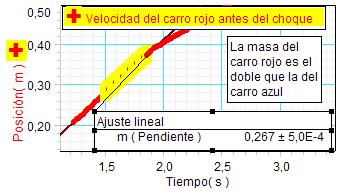
Para completar el trabajo, los grupos repiten el experimento alterando el valor relativo de las masas de los carros. La fotografía adjunta muestra el carro rojo con un sobrepeso, que es exactamente igual a su masa (250g). Así, la masa de este carro es el doble que la del otro carro azul y se ha de cumplir: p_antes = p_después → 2mv_{carro-rojo-antes} = 3mv_{conjunto-después}

Es decir, la velocidad del conjunto después del choque debe ser en este caso 2/3 de la velocidad que tiene el carro rojo antes de chocar.

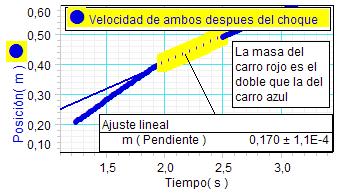
Los resultados obtenidos (a la izquierda) vuelven a confirmar la hipótesis con un buen grado de fiabilidad, puesto que el valor experimental de la velocidad del conjunto tras el choque, 0.170m/s, vuelve a diferir en menos de un 5% del valor esperado, 0.178m/s (0,267·2/3).

ARCHIVOS DE DATASTUDIO: Puedes descargar los resultados originales del experimento descrito en esta página. Para abrir los archivos se necesita el programa DataStudio, del que tienen licencia bastantes Departamentos de Física y Química de Institutos de Enseñanza Secundaria.