|
|
|
 |
|
RODADURA DE UN CARRITO
POR UN PLANO INCLINADO (I) |
|
|
| Experimentos
realizados por alumnos de Secundaria y de Bachillerato en el IES "Leonardo Da Vinci" de Alicante
|
|
|
| |
| |
|
 |
PLANTEAMIENTO,
HIPÓTESIS Y DISEÑO EXPERIMENTAL |
 |
 |
|
 |
GRÁFICAS DEL MOVIMIENTO
|
|
 |
OBTENCIÓN DE
LA ACELERACIÓN Y OTRAS MAGNITUDES NECESARIAS EN EL
EXPERIMENTO CON MODELLUS |
|
 |
CAMBIO DEL SISTEMA DE REFERENCIA. REPRESENTACIÓN DE LA
POSICIÓN FRENTE AL CUADRADO DEL TIEMPO |
|
 |
ARCHIVOS DE
DATASTUDIO |
|
| |
|
| |
|
|
|
PLANTEAMIENTO, HIPÓTESIS Y DISEÑO
EXPERIMENTAL |
| |
| |
|
Nos planteamos estudiar el movimiento de un
carrito que rueda por un plano inclinado. Los estudiantes
comienzan describiendo cualitativamente el movimiento (que
presumen uniformemente acelerado) y dibujando, a modo de
hipótesis, unas gráficas cualitativas de la posición, la
velocidad y la aceleración.
El objetivo del experimento es contrastar
estas hipótesis trabajando con los sensores y, si se confirma que el movimiento es
uniformemente acelerado, obtener la aceleración. Una
segunda
parte del experimento consistirá en crear una animación
adecuada para analizar la concordancia entre el
movimiento real del carrito y un movimiento virtual que responda
a las leyes deducibles del estudio con los sensores. |
| |
|
 |
|
En cuanto al diseño experimental, los
grupos usan un carril de los habituales en el
laboratorio para carritos, optando algunos por colocar
el sensor de movimiento al inicio del recorrido (en la
parte alta del plano inclinado) y otros por hacerlo en
el otro extremo, al final del recorrido.
La experiencia
acumulada en el manejo de los sensores enseñó a los
estudiantes que para determinar posiciones con
mayor precisión conviene que la superficie del móvil que
se enfrenta al sensor sea plana y perpendicular a la
dirección del movimiento. Una forma de lograrlo es pegar
al extremo del carrito un trozo de cartulina. |
| |
|
Los grupos tienen que ser de no menos de menos tres
alumnos. Durante el experimento, un alumno utilizará
el ordenador, otro dejará rodar el carrito y el tercero ha de filmar el
movimiento. La filmación se
necesita en la segunda parte del experimento, destinada al
análisis del movimiento con Modellus. |
| |
|
|
|
|
| |
|
 |
| |
|
GRÁFICAS DEL MOVIMIENTO |
| |
|
|
| |
|
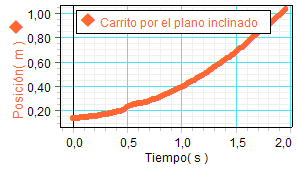 |
|
Después de conectar el sensor, el programa
genera una
gráfica vacía de la evolución de la posición, a la espera de
reflejar mediciones en el intervalo de tiempo transcurrido entre
dos clics del botón "Inicio".
Entrando en la ventana
de configuración del sensor, los equipos optan por trabajar con
una frecuencia de 50 Hz (es decir, 50 mediciones
de posición por
segundo). En principio se plantean obtener las gráficas de todas las
magnitudes cinemáticas, para lo que configuran el sensor para
dar valores de la posición la velocidad y la
aceleración. |
|
|
| |
|
|
| |
|
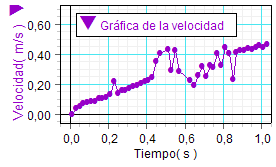 |
|
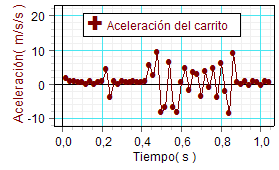 |
|
Como se observa, el perfil cualitativo de la gráficas
obtenidas de la posición corresponde muy bien con las hipótesis emitidas
previamente acerca del tipo de movimiento. Peor resulta
el aspecto de la gráfica de la velocidad y peor aún el
de la aceleración.
La razón de estos desajustes hay que
buscarla en el modo diferente de obtener la magnitud
experimental (posición) y las magnitudes derivadas
(velocidad y aceleración) |
|
|
| |
|
|
| |
El sensor mide únicamente valores de la
posición y deduce de ellos los correspondientes de la velocidad
y después de la aceleración. Cada imprecisión en una medición
directa de la posición se traslada (y así se van acumulando
errores) a las magnitudes derivadas (velocidad y luego, en mayor
grado, a la aceleración). Como consecuencia de ello el programa
llega a plantear algunos valores absurdos de la aceleración (por
ejemplo, negativos). No obstante, si se realizan ajustes
lineales sobre la velocidad y sobre la aceleración, los
resultados de dichos ajustes sí se corresponden con el tipo de
movimiento esperado (aunque proporcionan valores más
imprecisos que los obtenibles directamente de la gráfica de la
posición) |
|
| |
|
|
|
| |
|
 |
| |
|
OBTENCIÓN DE LA
ACELERACIÓN Y OTRAS MAGNITUDES NECESARIAS EN EL EXPERIMENTO CON
MODELLUS |
| |
| |
|
Con objeto de obtener
resultados cuantitativos, lo primero que hacen
los estudiantes es eliminar valores
experimentales que no corresponden al movimiento
de rodadura por el plano y/o valores que
adolecen de imprecisiones importantes. |
| |
|
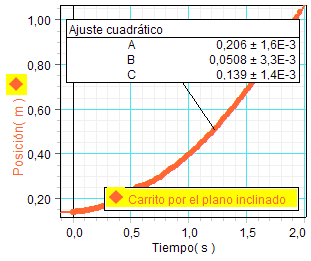 |
|
Sobre la gráfica así obtenida de la posición
realizan un ajuste cuadrático, puesto que la hipótesis
es suponer un movimiento uniformemente acelerado. Por la
misma razón realizan sendos ajustes lineales sobre
las gráficas de la velocidad y la aceleración.
Como se observa, el resultado fue satisfactorio, en la medida en que
el ajuste de la gráfica experimental
concuerda con la ecuación de un movimiento uniformemente
acelerado. Para atribuir un valor a la
aceleración, se realiza un ajuste cuadrático, puesto que
la hipótesis prevé un movimiento uniformemente
acelerado.
Resulta una
aceleración de 0,412 m/s2. Este es el
mejor valor que se puede obtener de esta magnitud, puesto
que, como hemos comentado, los valores de la evolución
de la velocidad y de la propia aceleración obtenidos por
el programa adolecen de mayor imprecisión que los de la
posición. |
|
| |
|
|
|
|
|
|
|
 |
|
|
|
CAMBIO DEL SISTEMA DE
REFERENCIA. REPRESENTACIÓN DE LA POSICIÓN FRENTE AL TIEMPO AL
CUADRADO |
| |
| |
|
 |
|
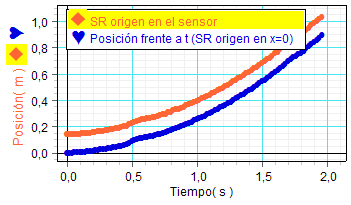
Resulta muy instructivo
estudiar la relación entre la posición y el
cuadrado del tiempo, para lo que, previamente interesa
desplazar el origen del sistema de referencia (SR) de
tal forma que sea x = 0 para t = 0 y nula la
velocidad inicial.
Para realizar dicho desplazamiento del origen del SR, se
utiliza la opción de calcular que proporciona el
programa y permite definir la nueva variable que
indicará la posición en dicho SR, x = xmedida
- xinicial. Después de hacerlo, la variable
calculada aparece en el lado izquierdo de la pantalla y
los estudiantes la arrastran para colocarla encima de la
posición anterior.
Se obtiene así la figura mostrada a
la izquierda, que enseña las gráficas del
movimiento en ambos SR. |
|
 |
|
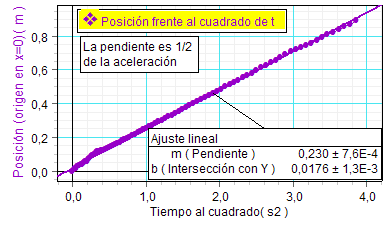
Del mismo modo, los
alumnos definen otra nueva variable para
calcular el cuadrado del tiempo. Y,
finalmente, representan la gráfica de la
posición (escrita en el SR con origen en
x = 0 para t = 0) respecto de
t2.
Puesto que el
movimiento estudiado se supone
uniformemente acelerado, dicha ecuación
es del tipo: x = (1/2)·a·t2
y procede realizar un ajuste lineal,
cuya pendiente m proporciona la
aceleración [m = a/2].
Obsérvese, por otra
parte, que el valor de la aceleración
que se obtiene por este procedimiento no
coincide con el valor más preciso que
obtiene el ajuste cuadrático realizado
directamente sobre la gráfica de la
posición. La razón hay que buscarla en
la imprecisiones introducidas por el
cálculo de t2 y de la
propia pendiente. |
|
| |
|
Para concluir el experimento, los
estudiantes apuntan la ecuación del movimiento que
proporciona el ajuste de la gráfica de la posición, así
como el valor experimental del ángulo. Esta información
es necesaria en la
segunda parte del análisis
experimental realizada con Modellus. |
|
|
|
|
|
|
|
|
|
 |
|
|
|
ARCHIVOS DE
DATASTUDIO: Te puedes descargar los
resultados originales del experimento que se
describe en esta página. Para abrir el archivo se necesita el programa
DataStudio, del que tienen
licencia bastantes departamentos de física y química de
institutos de enseñanza secundaria. |
|