|
|
|
 |
|
REALIZACIÓN DE TABLAS Y GRÁFICAS COMO TÉCNICA DE ANÁLISIS DE RESULTADOS
EXPERIMENTALES
|
|
|
| Experimentos
realizados por alumnos de Secundaria en el IES "Leonardo Da Vinci" de Alicante
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HIPÓTESIS SOBRE UNA RELACIÓN ENTRE
MAGNITUDES |
| |
| |
|
 |
|
Para interpretar los
datos experimentales obtenidos en un
proceso de investigación muchas veces interesa tabularlos y/o representarlos
gráficamente, con objeto de poner en
evidencia el tipo de dependencia
existente entre dos magnitudes. Para familiarizar a los estudiantes
con estas técnicas y promover que tomen
conciencia de su potencial utilidad, les
pedimos, en primer lugar, que emitan
hipótesis acerca de la relación que cabe
esperar entre la longitud de un cable de
plástico y su masa.
Pueden
desarrollar sus
hipótesis inventando
posibles valores de ambas magnitudes,
realizando una gráfica (cualitativa) de la relación, etc.
|
|
| |
|
|
|
|
| |
|
 |
| |
|
TABLA DE VALORES Y EXPRESIÓN OPERATIVA DE
LA RELACIÓN
|
| |
|
|
| |
|
 |
|
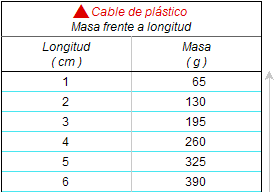
Tras poner en común las hipótesis emitidas
acerca de la relación entre la longitud de un
trozo de cable y su masa, aportamos una tabla de
valores incompleta de dicha relación. Los
estudiantes deben explicar cuantitativamente la
hipótesis y, luego, completar la tabla. |
|
|
|
|
 |
|
La ocasión es adecuada para
que aprendan a realizar la tabla con el
programa DataStudio y se les solicita también
que expresen matemáticamente la relación. En
este ejemplo, dicha relación es:
m = 65 · l
(l = longitud del pedazo de cable en cm;
m: masa del pedazo de cable en g)
Los estudiantes también expresan la relación verbalmente,
indicando que la masa
de cualquier pedazo del cable en cuestión es
proporcional a su longitud (siendo el factor de
proporcionalidad igual 65 g/cm) o, lo que
es equivalente, que cada incremento de longitud
del cable de 1 cm implica un aumento de
masa del mismo de 65 g. |
|
|
|
|
|
|
| |
|
 |
| |
|
REPRESENTACIÓN GRÁFICA DE LA RELACIÓN |
| |
| |
 |
|
 |
|
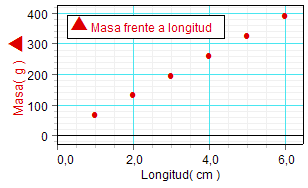
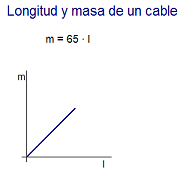
Los alumnos representan, por una parte, los valores
supuestos de la relación (figura de la
izquierda, construida
con DataStudio) y, por otra, la función
o ecuación matemática teórica a que
dichos valores se ajustan, m = 65·l
(figura de la derecha, obtenida con
Modellus). La longitud
(variable independiente) se indica en el eje de
abcisas y la masa (variable dependiente)
en el eje de ordenadas. La
representación obtenida es una recta
de pendiente positiva que pasa por el origen de
coordenadas, como corresponde a la
relación lineal o proporcional que se ha
supuesto entre la longitud y la masa de
cable. |
|
|
|
|
Por otro
lado, al hacer la representación gráfica,
interesa adoptar en cada eje una escala adecuada
para que la recta
no se incline excesivamente (lo que dificultaría
la visión de la propia gráfica). Tanto
cuando la realizan inicialmente a mano,
como después cuando usan el programa
Modellus, los estudiantes aprenden a
especificar dichas escalas que gradúan
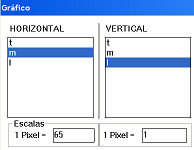
los ejes. Por ejemplo, si se desea que la recta sea
exactamente la bisectriz de ellos,
cada
división en el eje horizontal igual a
1 cm tiene la misma longitud que una
división en el eje vertical de 65 g. En
el programa Modellus esto
implica hacer que 1 pixel en la
representación horizontal sea igual a 65
pixeles en la representación vertical. |
|
 |
|
| |
|
|
|
|
| |
|
 |
| |
|
ANÁLISIS MATEMÁTICO A PARTIR DE LA GRÁFICA |
| |
|
|
| |
|
 |
|
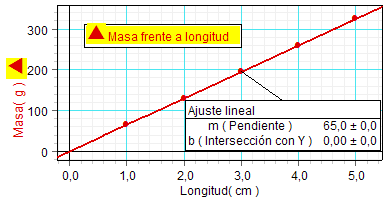
Sobre la gráfica que expresa
la relación entre la longitud y la masa de cable
(construida con DataStudio), los
estudiantes realizan un ajuste lineal, siguiendo
la hipótesis emitida acerca de dicha relación.
Dicho ajuste aporta la representación gráfica de
la ecuación teórica de la relación, y los
valores de las constantes m (pendiente,
igual a 65 g/m) y b (intersección
de la gráfica con el eje de abcisas, igual a
cero) que determinan dicha ecuación.
Obviamente,
en este caso el ajuste es exacto, si bien los
alumnos entienden que cuando los valores
representados procedan de un proceso experimental,
la relación teórica entre ellas no coincidirá
con los valores reales. |
|
|
|
|
|
|
| |
|
 |
|
|
|
ANIMACIONES MODELLUS DE REFUERZO |
| |
|
|
| |
|
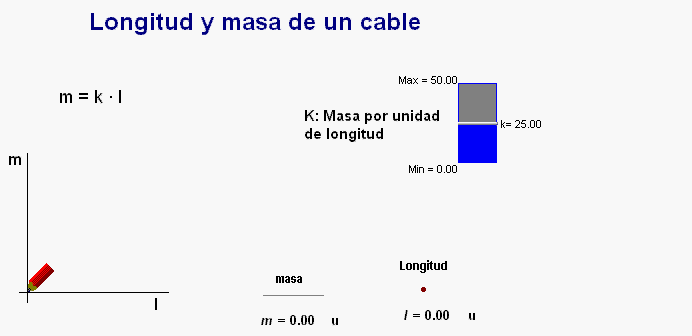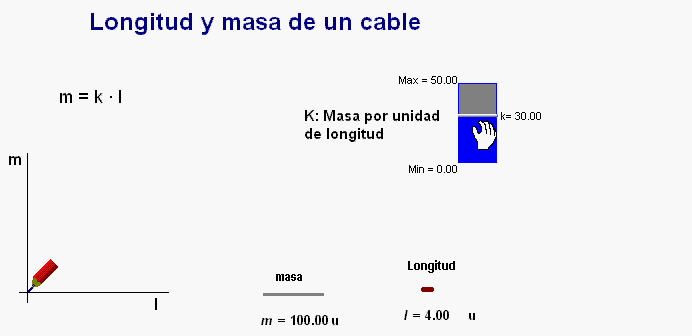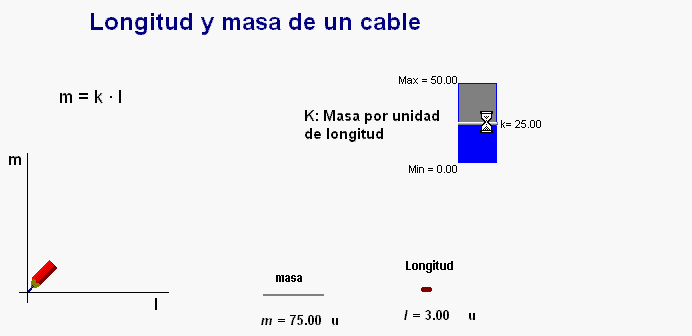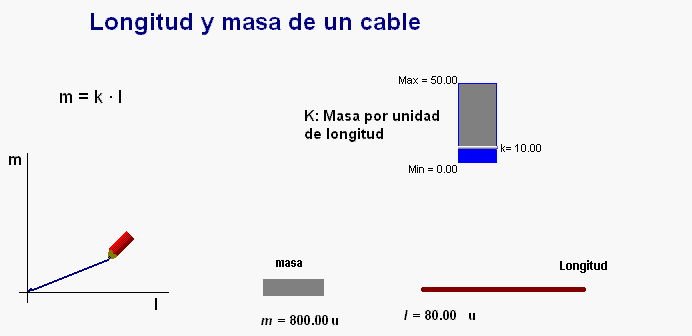
Para reforzar los conceptos
desarrollados en este trabajo, los alumnos
pueden trabajar con la animación
Modellus adjunta que dibuja la gráfica
de la relación entre la masa y la longitud de un
cable cualquiera.
Usando el controlador manual
disponible en la pantalla se pueden modificar el
valor de la k que indica la masa por unidad de
longitud para ver el
efecto que tiene que cambie dicho valor (es
decir, la pendiente) en la recta representada.
Clic
aquí para descargar la animación |
|
 |
| |
|
|
|
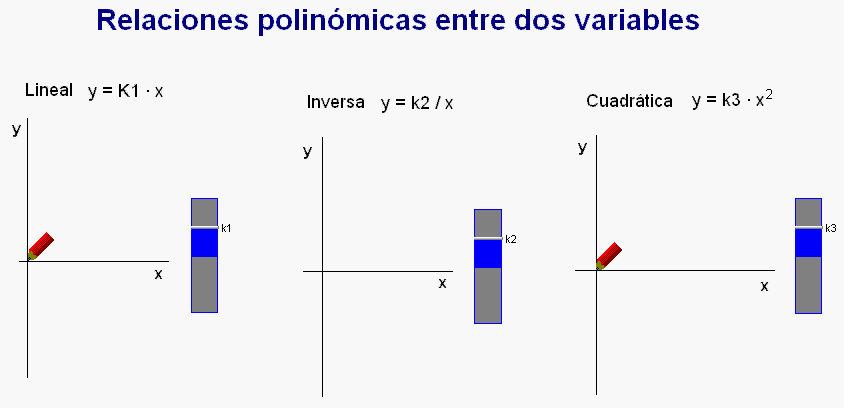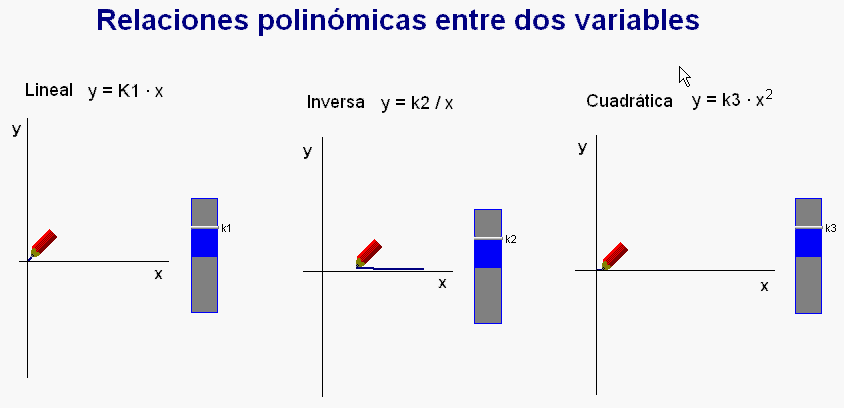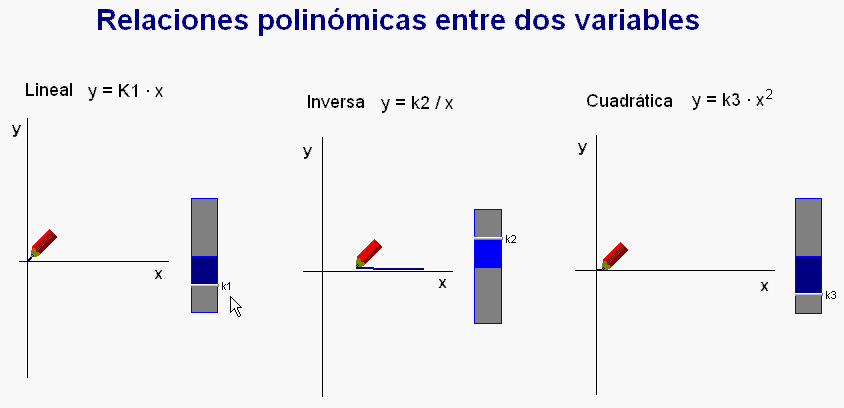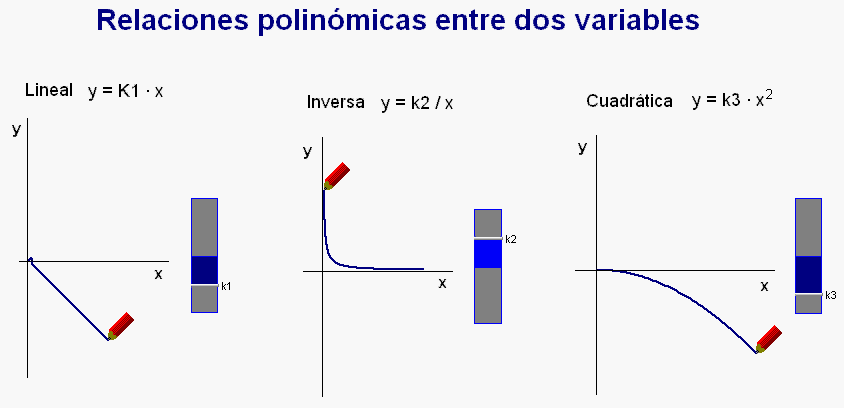
Finalmente, como complemento
a estos estudios centrados en observar un tipo
de relación entre variables,
introducimos otras relaciones posibles
entre las magnitudes, concretamente la
relación inversa, y la relación
cuadrática.
Para cada una, se exige a
los alumnos que expresen verbalmente
el tipo de relación, que "inventen"
valores posibles entre dos magnitudes
que la puedan cumplir, y que, luego los
representen gráficamente.
Todo ello se
puede ilustrar con la animación
Modellus adjunta (debajo).
Clic
aquí para descargar la animación
|
|
 |
|
|
| |
|
|
|
|
|
|
 |
|
|
|
 |
PROGRAMA DE ACTIVIDADES: Programa-guía de las actividades,
que se puede usar para realizar en el laboratorio este trabajo práctico. |
|
 |
ANIMACIONES:
Animaciones sobre la
ley de proporcionalidad directa y sobre
gráficas de algunas
relaciones polinómicas entre dos variables. |
|
 |
ARCHIVO DEL ANÁLISIS:
Resultados del análisis realizado con el programa DataStudio
sobre la
relación entre la longitud de un cable y su masa. |
|
|
|
|
 |



